
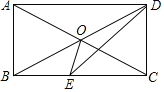
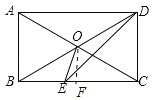
【题目】如图,在四边形ABCD中,AD∥BC,∠ABC=∠ADC,对角线AC、BD交于点O,AO=BO,DE平分∠ADC交BC于点E,连接OE.
(1)求证:四边形ABCD是矩形;
(2)若AB=2,求△OEC的面积.
【答案】(1)详见解析;(2)1
【解析】
(1)证出∠BAD=∠BCD,得出四边形ABCD是平行四边形,得出OA=OC,OB=OD,证出AC=BD,即可解决问题;
(2)作OF⊥BC于F.求出EC、OF即可解决问题;
(1)证明:∵AD∥BC,
∴∠ABC+∠BAD=180°,∠ADC+∠BCD=180°,
∵∠ABC=∠ADC,
∴∠BAD=∠BCD,
∴四边形ABCD是平行四边形,
∴OA=OC,OB=OD,
∵OA=OB,
∴AC=BD,
∴四边形ABCD是矩形.
(2)解:作OF⊥BC于F,如图所示.
∵四边形ABCD是矩形,
∴CD=AB=2,∠BCD=90°,AO=CO,BO=DO,AC=BD,
∴AO=BO=CO=DO,
∴BF=FC,
∴OF=![]() CD=1,
CD=1,
∵DE平分∠ADC,∠ADC=90°,
∴∠EDC=45°,
在Rt△EDC中,EC=CD=2,
∴△OEC的面积=![]() ECOF=1.
ECOF=1.


科目:初中数学 来源: 题型:
【题目】定义:经过三角形一边中点,且平分三角形周长的直线叫做这个三角形在该边上的中分线,其中落在三角形内部的部分叫做中分线段.
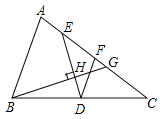
(1)如图,△ABC中,AC>AB,DE是△ABC在BC边上的中分线段,F为AC中点,过点B作DE的垂线交AC于点G,垂足为H,设AC=b,AB=c.
①求证:DF=EF;
②若b=6,c=4,求CG的长度;
(2)若题(1)中,S△BDH=S△EGH,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某大桥采用低塔斜拉桥桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2米,两拉索底端距离AD为20米,请求出立柱BH的长.(结果精确到0.1米, ![]() ≈1.73)
≈1.73)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,且AB=12,点C为半圆上的一点.将此半圆沿BC所在的直线折叠,若圆弧BC恰好过圆心O,则图中阴影部分的面积是( )

A. 4πB. 5πC. 6πD. 8π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】江门旅游文化节开幕前,某茶叶公司预测今年茶叶能够畅销,就用32000元购进了一批茶叶,上市后很快脱销,茶叶公司又用68000元购进第二批茶叶,所购数量是第一批购进数量的2倍,但每千克茶叶进价多了10元.
(1)该茶叶公司两次共购进这种茶叶多少千克?
(2)如果这两批茶叶每千克的售价相同,且全部售完后总利润率不低于20%,那么每千克售价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
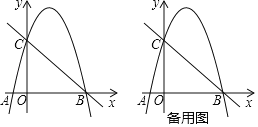
【题目】如图,二次函数y=ax2﹣3ax+c的图象与x轴交于点A、B,与y轴交于点C直线y=﹣x+4经过点B、C.
(1)求抛物线的表达式;
(2)过点A的直线交抛物线于点M,交直线BC于点N.
①点N位于x轴上方时,是否存在这样的点M,使得AM:NM=5:3?若存在,求出点M的坐标;若不存在,请说明理由.
②连接AC,当直线AM与直线BC的夹角∠ANB等于∠ACB的2倍时,请求出点M的横坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
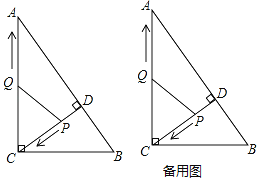
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D,点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.
(1)求线段CD的长;
(2)当△CPQ与△BDC相似时,求t值;
(3) 设△CPQ的面积为y,求y与t的函数关系式,并判断△PCQ的面积是否有最大值还是最小值?若有,求出t为何值时y的最值,若没有,则说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
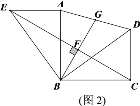
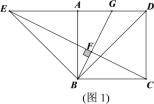
【题目】如图,四边形ABCD中,CD∥AB,∠ABC=90°,AB=BC,将△BCD绕点B逆时针旋转90°得到△BAE,连接CE,过点B作BG⊥CE于点F,交AD于点G.
(1)如图1,CD=AB.
①求证:四边形ABCD是正方形;
②求证:G是AD中点;
(2)如图2,若CD<AB,请判断G是否仍然是AD的中点?若是,请证明:若不是,请说理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若一个三角形一条边的平方等于另两条边的乘积,我们把这个三角形叫做比例三角形.
![]() 已知
已知![]() 是比例三角形,
是比例三角形,![]() ,
,![]() ,请直接写出所有满足条件的AC的长;
,请直接写出所有满足条件的AC的长;
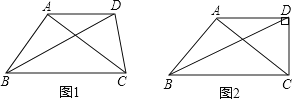
![]() 如图1,在四边形ABCD中,
如图1,在四边形ABCD中,![]() ,对角线BD平分
,对角线BD平分![]() ,
,![]() 求证:
求证:![]() 是比例三角形.
是比例三角形.
![]() 如图2,在
如图2,在![]() 的条件下,当
的条件下,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com