
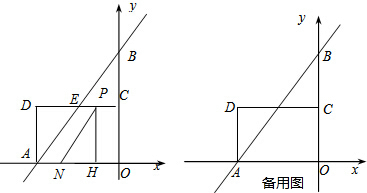
���� ��1���ֱ���x��y����0�����������A���B�����꣬���ı���AOCDΪ���Σ���֪��CD��x�ᣬ������֪��D��C��E�������������ͬ���ɵ�CΪOB���е㣬�����C�����꣬Ȼ��C�����������ֱ��y=$\frac{4}{3}$x+4������ֱ��AB��CD����E�����ꣻ
��2���ٷ�����������ۣ���һ���������0��t��2ʱ���ڶ����������2��t��6ʱ��
���ɵ�Q�ǵ�B���ڵ�A�ĶԳƵ㣬�������Q�����꣬Ȼ������PB��CH���ɵ��ı���PHCB��ƽ���ı��Σ������ɵã�PB=CH�������ɽ�BP+PH+HQת��ΪCH+HQ+2��Ȼ���������֮���߶���̿�֪������C��H��Q��ͬһֱ����ʱ��CH+HQ��ֵ��С��Ȼ�����ֱ��CQ�Ĺ�ϵʽ�����������ֱ��CQ��x��Ľ���H�����꣬�Ӷ����������P������
��� �⣺��1����ֱ��y=$\frac{4}{3}$x+4�ֱ�x�ᣬy����A��B���㣬
����x=0�ã�y=4��
��y=0�ã�x=-3��
��A��-3��0����B��0��4����
��OA=3��OB=4��
�ߵ�CΪOB���е㣬
��OC=2��
��C��0��2����
���ı���AOCDΪ���Σ�
��OA=CD=3��OC=AD=2��CD��OA��x�ᣩ��
��D��C��E�������������ͬ��
���E��������Ϊ2����y=2����ֱ��y=$\frac{4}{3}$x+4�ã�x=-1.5��
��E��-1.5��2����
��2���ٷ�����������ۣ�
��һ�������0��t��1.5ʱ����ͼ1��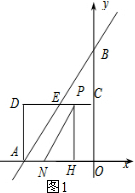
���������֪������t�룬CP=t��AN=t��HO=CP=t��PH=OC=2��
��NH=3-2t��
��S��NPH=$\frac{1}{2}$PH•NH���ҡ�NPH�����Ϊ1��
��$\frac{1}{2}$��2����3-2t��=1��
��ã�t=1��
�ڶ����������1.5��t��3ʱ����ͼ2��
���������֪������t�룬CP=t��AN=t��HO=CP=t��PH=OC=2��
��AH=3-t��
��HN=AN-AH=t-��3-t��=2t-3��
��S��NPH=$\frac{1}{2}$PH•NH���ҡ�NPH�����Ϊ1��
��$\frac{1}{2}$��2����2t-3��=1��
��ã�t=2��
�൱t=1��2ʱ�����ڡ�NPH�����Ϊ1��
��BP+PH+HQ����Сֵ��
����PB��CH��HQ�����ı���PHCB��ƽ���ı��Σ���ͼ3��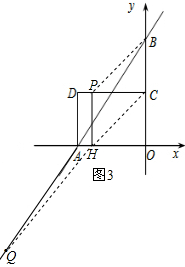
���ı���PHCB��ƽ���ı��Σ�
��PB=CH��
��BP+PH+HQ=CH+HQ+2��
��BP+PH+HQ����Сֵ����CH+HQ+2����Сֵ��
��ֻ��CH+HQ��С���ɣ�
������֮���߶���̣�
�൱��C��H��Q��ͬһֱ����ʱ��CH+HQ��ֵ��С��
����Q��QM��y�ᣬ����ΪM��
�ߵ�Q�ǵ�B���ڵ�A�ĶԳƵ㣬
��OA�ǡ�BQM����λ�ߣ�
��QM=2OA=6��OM=OB=4��
��Q��-6��-4����
��ֱ��CQ�Ĺ�ϵʽΪ��y=kx+b��
��C��0��2����Q��-6��-4���ֱ������ʽ�ã�
$\left\{\begin{array}{l}{b=2}\\{-6k+b=-4}\end{array}\right.$��
��ã�$\left\{\begin{array}{l}{b=2}\\{k=1}\end{array}\right.$��
��ֱ��CQ�Ĺ�ϵʽΪ��y=x+2��
��y=0�ã�x=-2��
��H��-2��0����
��PH��y�ᣬ
��P��-2��2����
���� ������һ�κ������ۺ��⣬��Ҫ�����ˣ��ô���ϵ������һ�κ�����ϵʽ��һ�κ�����x�ᡢy�ύ������������߶ι�������ֵ����ȣ��⣨2���Т���Ĺؼ��ǣ�����������������ۣ��⣨2���Т���Ĺؼ��ǣ���������֮���߶���̣������ֵ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
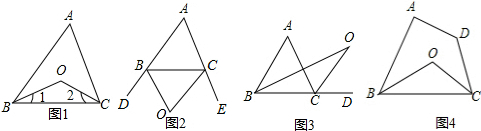
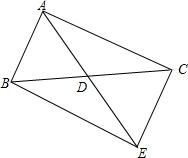 ��ͼ���ڡ�ABC�У�ADΪBC���ϵ����ߣ��ӳ�AD��E��ʹDE=AD������BE��CE
��ͼ���ڡ�ABC�У�ADΪBC���ϵ����ߣ��ӳ�AD��E��ʹDE=AD������BE��CE�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
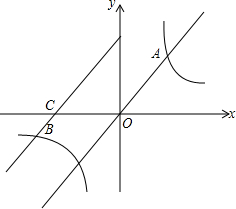 ��ͼ��ֱ��y=2x��˫����y=$\frac{k}{x}$���ڵ�A����ֱ��y=2x����ƽ��������λ����˫����y=$\frac{k}{x}$����һ��֧���ڵ�B����x�ύ�ڵ�C����֪$\frac{BC}{OA}$=$\frac{1}{2}$����ôk=32��
��ͼ��ֱ��y=2x��˫����y=$\frac{k}{x}$���ڵ�A����ֱ��y=2x����ƽ��������λ����˫����y=$\frac{k}{x}$����һ��֧���ڵ�B����x�ύ�ڵ�C����֪$\frac{BC}{OA}$=$\frac{1}{2}$����ôk=32���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
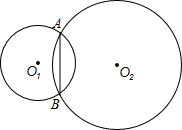 ��ͼ�����ཻԲ�Ĺ�����AB���ڡ�O1��Ϊ�ڽ��������ε�һ�ߣ��ڡ�O2��Ϊ�ڽ��������ε�һ�ߣ�������Բ�����֮�ȣ�
��ͼ�����ཻԲ�Ĺ�����AB���ڡ�O1��Ϊ�ڽ��������ε�һ�ߣ��ڡ�O2��Ϊ�ڽ��������ε�һ�ߣ�������Բ�����֮�ȣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ���ѡ�ABC�Ƶ�C��ʱ����ת90��õ���DCE������A=35�㣬���ADEΪ��������
��ͼ���ѡ�ABC�Ƶ�C��ʱ����ת90��õ���DCE������A=35�㣬���ADEΪ��������| A�� | 35�� | B�� | 55�� | C�� | 135�� | D�� | 125�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
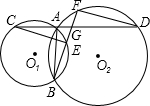 ��ͼ����֪��O1�͡�O2�ཻ��A��B���㣬��A��ֱ�߽���Բ��C��D���㣬��B ��ֱ�߽���Բ��E��F���㣬CD��EF���ڵ�G������DF��CE��GΪCD���е㣮��֤��CE=DF��
��ͼ����֪��O1�͡�O2�ཻ��A��B���㣬��A��ֱ�߽���Բ��C��D���㣬��B ��ֱ�߽���Բ��E��F���㣬CD��EF���ڵ�G������DF��CE��GΪCD���е㣮��֤��CE=DF���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com