
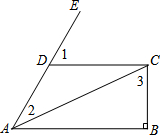
 如图,CD∥AB,CB⊥AB,∠1=60°,∠2=40°,则∠3=70°.
如图,CD∥AB,CB⊥AB,∠1=60°,∠2=40°,则∠3=70°. 科目:初中数学 来源: 题型:选择题
| A. | 9.27×109 | B. | 92.7×108 | C. | 9.27×1010 | D. | 0.927×1010 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
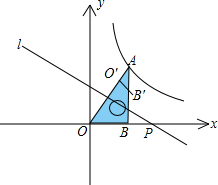 如图,在平面直角坐标系中,点A在第一象限,AB⊥x轴,B(2,0),tan∠AOB=$\sqrt{3}$,过点A的双曲线为y=$\frac{k}{x}$,在x轴上取一点P,过x轴正半轴上的点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的对应线段O′B′.
如图,在平面直角坐标系中,点A在第一象限,AB⊥x轴,B(2,0),tan∠AOB=$\sqrt{3}$,过点A的双曲线为y=$\frac{k}{x}$,在x轴上取一点P,过x轴正半轴上的点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的对应线段O′B′.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
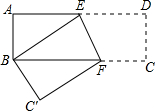 将矩形纸片ABCD按下图方式折叠,使点D与点B重合,折痕为EF,若S△ABE:S△BFE=4:5,则tan∠BFE=( )
将矩形纸片ABCD按下图方式折叠,使点D与点B重合,折痕为EF,若S△ABE:S△BFE=4:5,则tan∠BFE=( )| A. | $\frac{1}{3}$ | B. | $\sqrt{3}$ | C. | 3 | D. | $3\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| A型利润 | B型利润 | |
| 甲店 | 200 | 170 |
| 乙店 | 160 | 150 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com