
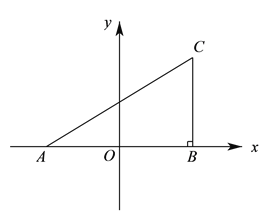
【题目】如图①,在平面直角坐标系中, ![]() ,
, ![]() ,且满足
,且满足![]() ,过
,过![]() 作
作![]() 轴于
轴于![]() .
.
(![]() )求
)求![]() 的面积.
的面积.
(![]() )在
)在![]() 轴上是否存在点
轴上是否存在点![]() ,使
,使![]() 和
和![]() 的面积相等?若存在,求出
的面积相等?若存在,求出![]() 点坐标;若不存在,说明理由.
点坐标;若不存在,说明理由.
(![]() )动点
)动点![]() 从点
从点![]() 出发,以每秒
出发,以每秒![]() 的速度沿射线
的速度沿射线![]() 运动,如果在运动过程中
运动,如果在运动过程中![]() 为等腰三角形,求出点
为等腰三角形,求出点![]() 运动的时间.
运动的时间.
【答案】见解析.
【解析】试题分析:(1)根据非负数的性质易得a=-2,b=2,然后根据三角形面积公式计算即可;(2)分①当![]() 点在
点在![]() 轴正半轴上时和②当
轴正半轴上时和②当![]() 点在
点在![]() 轴负半轴上时两种情况求点P的坐标;(3)可分①当
轴负半轴上时两种情况求点P的坐标;(3)可分①当![]() 时;②当
时;②当![]() 时;③当
时;③当![]() 时三种情况求点
时三种情况求点![]() 运动的时间.
运动的时间.
试题解析:
(![]() )∵
)∵![]() ,
,
![]() ,
, ![]() ,
,
∴![]() ,
, ![]() .
.
∴![]() ,
, ![]() .
.
∴![]() ,
, ![]() .
.
∵![]() 轴于点
轴于点![]() .
.
∴![]() .
.
∴![]() .
.
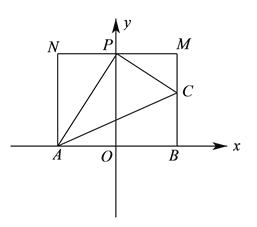
(![]() )①当
)①当![]() 点在
点在![]() 轴正半轴上时,设
轴正半轴上时,设![]() .
.
∴![]() .
.
如图所示,过![]() 作
作![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴.
轴.
∴![]() ,
,
![]() .
.
∴![]()
![]()
![]()
![]() .
.
解得![]() .
.
∴![]() .
.
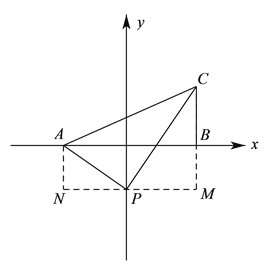
②当![]() 点在
点在![]() 轴负半轴上时,设
轴负半轴上时,设![]() .
.
∴![]() .
.
如图所示,过![]() 作
作![]() 轴,
轴, ![]() 轴,
轴, ![]() 轴.
轴.
∴![]() ,
,
![]() .
.
![]() .
.
∴![]()
![]()
![]()
![]() .
.
解得![]() .
.
∴![]() ,
,
综上, ![]() 的坐标为
的坐标为![]() 或
或![]() .
.
(![]() )①当
)①当![]() 时,
时,
![]() .
.
∴![]() .
.
②当![]() 时,
时,
∵![]() 是等腰三角形,
是等腰三角形,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
③当![]() 时,
时,
设![]() .
.
∴![]() .
.
在![]() 中,
中, ![]() .
.
∴![]() .
.
解得![]() .
.
∴![]() ,
,
∴![]() .
.
综上![]() 或
或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,过y轴上任意一点p,作x轴的平行线,分别与反比例函数y=-![]() 和y=
和y=![]() 的图象交于A点和B点.若C为x轴上任意一点,连接AC、BC,则△ABC的面积为 .
的图象交于A点和B点.若C为x轴上任意一点,连接AC、BC,则△ABC的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
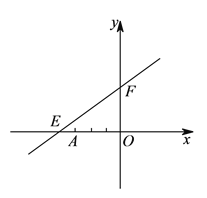
【题目】如图,直线![]() 与
与![]() 轴
轴![]() 轴分别交于点
轴分别交于点![]() 、
、![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
(![]() )求
)求![]() 的值.
的值.
(![]() )若点
)若点![]() 是第二象限内的直线
是第二象限内的直线![]() 上的一个动点,在点
上的一个动点,在点![]() 的运动过程中,试写出
的运动过程中,试写出![]() 的面积
的面积![]() 与
与![]() 的函数关系式,并写出自变量
的函数关系式,并写出自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列解题过程:已知![]() 、
、![]() 、
、![]() 为△ABC的三边,且满足
为△ABC的三边,且满足![]() ,
,
试判断△ABC的形状.
解:∵![]() ①
①
∴![]() ②
②
∴![]() ③
③
∴△ABC为直角三角形.
问:(1)上述解题过程,从哪一步开始出现错误?请写出该步的代号________;
(2)错误的原因是____________________________;
(3)本题的正确结论是_________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AC=BC,∠ACB=90°,CE是过C点的一条直线,AD⊥CE于D,BE⊥CE于E,DE=4cm,AD=2cm,则BE=( )
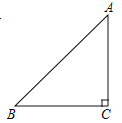
A. 2cm B. 4cm C. 6cm或2cm D. 6cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证( )

A. (a+b)2=a2+2ab+b2
B. (a﹣b)2=a2﹣2ab+b2
C. a2﹣b2=(a+b)(a﹣b)
D. (a+2b)(a﹣b)=a2+ab﹣2b2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知图1将线段AB向右平移1个单位长度,图2是将线段AB折一下再向右平移1个单位长度,请在图3中画出一条有两个折点的折线向右平移1个单位长度的图形;
(2)若长方形的长为a,宽为b,请分别写出三个图形中除去阴影部分后剩下部分的面积;
(3)如图4,在宽为10 m,长为40 m的长方形菜地上有一条弯曲的小路,小路宽度为1 m,求这块菜地的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在下列条件中,不能作为判断△ABD≌△BAC的条件是( )

A. ∠D=∠C,∠BAD=∠ABC B. ∠BAD=∠ABC,∠ABD=∠BAC
C. BD=AC,∠BAD=∠ABC D. AD=BC,BD=AC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com