
科目:初中数学 来源: 题型:解答题
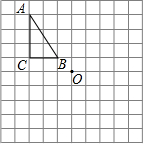 已知,如图△ABC,请在网格纸中画.
已知,如图△ABC,请在网格纸中画.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
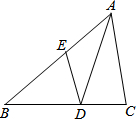 如图,在△ABC中,AD是角平分线,点E在AB上,且DE∥CA.
如图,在△ABC中,AD是角平分线,点E在AB上,且DE∥CA.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
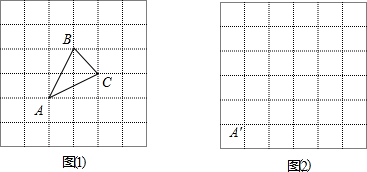
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明和小刚用如图的两个转盘做配紫色的游戏,游戏规则是:分别旋转两个转盘,若其中的一个转盘转出了红色,另一个转出了蓝色,则可以配成紫色.此时小刚得1分,否则小明得1分.此游戏规则公平吗?请说明理由.
小明和小刚用如图的两个转盘做配紫色的游戏,游戏规则是:分别旋转两个转盘,若其中的一个转盘转出了红色,另一个转出了蓝色,则可以配成紫色.此时小刚得1分,否则小明得1分.此游戏规则公平吗?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
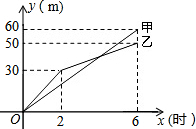 在三河市创建文明城区的活动中,有两段长度相等的彩色道砖铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设彩色道砖的长度y(米)与施工时间x(时)之间关系的部分图象.请解答下列问题:
在三河市创建文明城区的活动中,有两段长度相等的彩色道砖铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设彩色道砖的长度y(米)与施工时间x(时)之间关系的部分图象.请解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
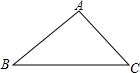 某厂有一块如图所示的△ABC铜板,根据需要,现要把它加工成一个平行四边形铜板,要把材料完全利用起来,可怎样加工?请你利用学过的知识帮助工人师傅把切割的线用虚线画出来,并指出加工后的平行四边形,能否将此三角形铜板加工成长方形?请给出说明.
某厂有一块如图所示的△ABC铜板,根据需要,现要把它加工成一个平行四边形铜板,要把材料完全利用起来,可怎样加工?请你利用学过的知识帮助工人师傅把切割的线用虚线画出来,并指出加工后的平行四边形,能否将此三角形铜板加工成长方形?请给出说明.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com