
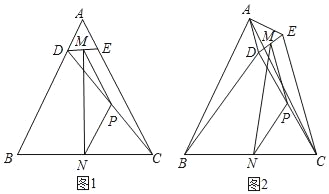
【题目】如图1,△ABC中,AB=AC=6,BC=4,点D、E分别在边AB、AC上,且AD=AE=1,连接DE、CD,点M、N、P分别是线段DE、BC、CD的中点,连接MP、PN、MN.
(1)求证:△PMN是等腰三角形;
(2)将△ADE绕点A逆时针旋转,
①如图2,当点D、E分别在边AC两侧时,求证:△PMN是等腰三角形;
②当△ADE绕点A逆时针旋转到第一次点D、E、C在一条直线上时,请直接写出此时BD的长.
【答案】(1)见解析;(2)①见解析;②![]() .
.
【解析】
(1)利用三角形的中位线得出PM=![]() CE,PN=
CE,PN=![]() BD,进而判断出BD=CE,即可得出结论PM=PN;
BD,进而判断出BD=CE,即可得出结论PM=PN;
(2)①先证明△ABD≌△ACE,得BD=CE,同理根据三角形中位线定理可得结论;
②如图4,连接AM,计算AN和DE、EM的长,如图3,证明△ABD≌△CAE,得BD=CE,根据勾股定理计算CM的长,可得结论
(1)如图1,∵点N,P是BC,CD的中点,
∴PN∥BD,PN=![]() BD,
BD,
∵点P,M是CD,DE的中点,
∴PM∥CE,PM=![]() CE,
CE,
∵AB=AC,AD=AE,
∴BD=CE,
∴PM=PN,
∴△PMN是等腰三角形;
(2)①如图2,∵∠DAE=∠BAC,
∴∠BAD=∠CAE,
∵AB=AC,AD=AE,
∴△ABD≌△ACE,
∵点M、N、P分别是线段DE、BC、CD的中点,
∴PN=![]() BD,PM=
BD,PM=![]() CE,
CE,
∴PM=PN,
∴△PMN是等腰三角形;
②当△ADE绕点A逆时针旋转到第一次点D、E、C在一条直线上时,如图3,
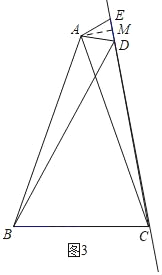
∵∠BAC=∠DAE,
∴∠BAD=∠CAE,
∵AB=AC,AD=AE,
∴△ABD≌△CAE,
∴BD=CE,
如图4,连接AM,
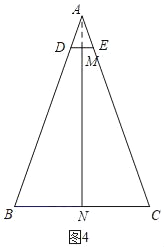
∵M是DE的中点,N是BC的中点,AB=AC,
∴A、M、N共线,且AN⊥BC,
由勾股定理得:AN=![]() =4
=4![]() ,
,
∵AD=AE=1,AB=AC=6,
∴![]() =
=![]() ,∠DAE=∠BAC,
,∠DAE=∠BAC,
∴△ADE∽△AEC,
∴![]() ,
,
∴![]() ,
,
∴AM=![]() ,DE=
,DE=![]() ,
,
∴EM=![]() ,
,
如图3,Rt△ACM中,CM=![]() =
=![]() =
=![]() ,
,
∴BD=CE=CM+EM=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,点A,B为定点,定直线l//AB,P是l上一动点.点M,N分别为PA,PB的中点,对于下列各值:
①线段MN的长;
②△PAB的周长;
③△PMN的面积;
④直线MN,AB之间的距离;
⑤∠APB的大小.
其中会随点P的移动而变化的是( )

A. ②③ B. ②⑤ C. ①③④ D. ④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线交AB于点E,交AC的延长线于点F.
(1)求证:DE⊥AB;
(2)若tan∠BDE=![]() , CF=3,求DF的长.
, CF=3,求DF的长.
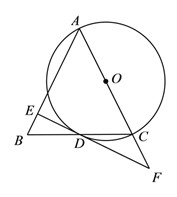
查看答案和解析>>
科目:初中数学 来源: 题型:
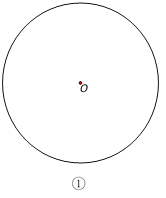
【题目】(问题提出)
求证:如果一个定圆的内接四边形对角线互相垂直,那么这个四边形每组对边的平方和是一个定值.
(从特殊入手)
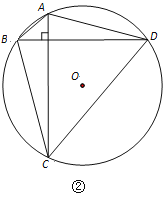
我们不妨设定圆O的半径是R,⊙O的内接四边形ABCD中,AC⊥BD.请你在图①中补全特殊位置时的图形,并借助于所画图形探究问题的结论.
(问题解决)
已知:如图②,定圆⊙O的半径是R,四边形ABCD是⊙O的内接四边形, AC⊥BD.
求证: .
证明:
查看答案和解析>>
科目:初中数学 来源: 题型:
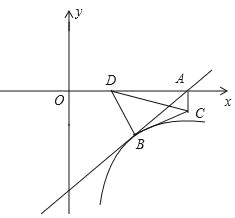
【题目】如图,在平面直角坐标系中,直线y=kx﹣10经过点A(12,0)和B(a,﹣5),双曲线y=![]() 经过点B.
经过点B.
(1)求直线y=kx﹣10和双曲线y=![]() 的函数表达式;
的函数表达式;
(2)点C从点A出发,沿过点A与y轴平行的直线向下运动,速度为每秒1个单位长度,点C的运动时间为t(0<t<12),连接BC,作BD⊥BC交x轴于点D,连接CD,
①当点C在双曲线上时,求t的值;
②在0<t<6范围内,∠BCD的大小如果发生变化,求tan∠BCD的变化范围;如果不发生变化,求tan∠BCD的值.
③当DC=![]() 时,请直接写出t的值.
时,请直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,点E是BC边的中点,连接AE并延长与DC的延长线交于F.
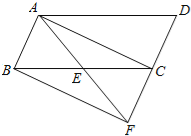
(1)求证:CF=CD;
(2)若AF平分∠BAD,连接DE,试判断DE与AF的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
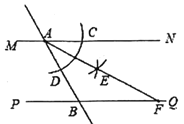
【题目】如图,直线![]() ,直线
,直线![]() 分别与
分别与![]() ,
,![]() 相交于点
相交于点![]() 、
、![]() ,小宇同学利用尺规按以下步骤作图:①以点
,小宇同学利用尺规按以下步骤作图:①以点![]() 为圆心,以任意长为半径作弧交
为圆心,以任意长为半径作弧交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ②分别以
②分别以![]() ,
,![]() 为圆心,以大于,
为圆心,以大于,![]() 长为半径作弧,两弧在
长为半径作弧,两弧在![]() 内交于点
内交于点![]() ;③作射线
;③作射线![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,则
,则![]() ____________.
____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题情境】
如图1,四边形ABCD是正方形,M是BC边上的一点,E是CD边的中点,AE平分∠DAM.

【探究展示】
(1)证明:AM=AD+MC;
(2)AM=DE+BM是否成立?若成立,请给出证明;若不成立,请说明理由.
【拓展延伸】
(3)若四边形ABCD是长与宽不相等的矩形,其他条件不变,如图2,探究展示(1)、(2)中的结论是否成立?请分别作出判断,不需要证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com