
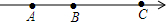
分析 (1)根据非负数的性质求得a=-3,b=9;
(2)分C点在线段AB上和线段AB的延长线上两种情况讨论即可求解;
(3)当P与点B重合时,|x-a|+|x-b|+|x-c|即当x=b时,取得最小值;
(4)分当0<t≤4时,当t>4时,表示出甲、乙两小球之间的距离d即可.
解答 解:(1)∵|a+3|+(c-9)2=0,
∴a+3=0,c-9=0,
解得,a=-3,b=9;
(2)数轴上点B表示的数为b.
∵BC=2AB,
∴|c-b|=2|b-a|,
即9-b=2[b-(-3)]
解得:b=1;
(3)当x=b=1时,
|x-a|+|x-b|+|x-c|=|x-(-3)|+|x-1|+|x-9|=12为最小值;
(4)当t不超过4秒(或表述为0≤t≤4或4秒以前),d=12-t;
当t超过4秒(或表述为t>4或4秒以后),d=3t-4.
点评 此题考查是列代数式,数轴上两点之间的距离,掌握两地之间的距离求法是解决问题的关键.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
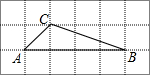 如图,A,B,C三点在正方形网络线的交点处,则tanB的值为( )
如图,A,B,C三点在正方形网络线的交点处,则tanB的值为( )| A. | $\frac{1}{3}$ | B. | 3 | C. | $\frac{{\sqrt{10}}}{3}$ | D. | $\frac{{\sqrt{10}}}{10}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知这是一座圆弧形涵洞的入口的示意图,涵洞的最高点C到地面AB的距离为6米,涵洞入口地面的宽度AB为4米,请你求这座涵洞圆弧所在圆的半径长.
如图,已知这是一座圆弧形涵洞的入口的示意图,涵洞的最高点C到地面AB的距离为6米,涵洞入口地面的宽度AB为4米,请你求这座涵洞圆弧所在圆的半径长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com