
【题目】一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为![]() 千米,出租车离甲地的距离为
千米,出租车离甲地的距离为![]() 千米,两车行驶的时间为
千米,两车行驶的时间为![]() 小时,
小时,![]() 、
、![]() 关于
关于![]() 的函数图像如图所示:
的函数图像如图所示:
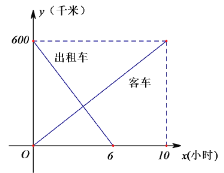
(1)根据图像,求出![]() 、
、![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)设两车之间的距离为![]() 千米.
千米.
①求两车相遇前![]() 关于
关于![]() 的函数关系式;
的函数关系式;
②求出租车到达甲地后![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(3)甲、乙两地间有![]() 、
、![]() 两个加油站,相距200千米,若客车进入
两个加油站,相距200千米,若客车进入![]() 加油站时,出租车恰好进入
加油站时,出租车恰好进入![]() 加油站,求
加油站,求![]() 加油站离甲地的距离.
加油站离甲地的距离.
【答案】(1)y1=60x(0≤x≤10),y2=100x+600(0≤x≤6);(2)①S=y2y1=160x+600;②S=60x(6≤x≤10);(3)150km或300km.
【解析】
(1)直接运用待定系数法就可以求出y1、y2关于x的函数图关系式;
(2)①根据当0≤x<![]() 时,求出即可,②当6≤x≤10时,求出即可;
时,求出即可,②当6≤x≤10时,求出即可;
(3)分A加油站在甲地与B加油站之间,B加油站在甲地与A加油站之间两种情况列出方程求解即可.
解:(1)设y1=k1x,由图可知,函数图象经过点(10,600),
∴10k1=600,
解得:k1=60,
∴y1=60x(0≤x≤10),
设y2=k2x+b,由图可知,函数图象经过点(0,600),(6,0),则

解得:
![]()
∴y2=100x+600(0≤x≤6);
(2)①由题意,得
60x=100x+600
x=![]() ,即第
,即第![]() 小时两车相遇
小时两车相遇
当0≤x<![]() 时, S=y2y1=160x+600;
时, S=y2y1=160x+600;
②令y2=100x+600=0,解得:x=6
即第6小时出租车到达甲地
当6≤x≤10时,S=60x;
(3)由题意,得
①当A加油站在甲地与B加油站之间时,(100x+600)60x=200,
解得x=![]() ,
,
此时,A加油站距离甲地:60×![]() =150km,
=150km,
②当B加油站在甲地与A加油站之间时,60x(100x+600)=200,
解得x=5,此时,A加油站距离甲地:60×5=300km,
综上所述,A加油站到甲地距离为150km或300km.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,已知∠MON=30°,B为OM上一点,BA⊥ON于A,四边形ABCD为正方形,P为射线BM上一动点,连结CP,将CP绕点C顺时针方向旋转90°得CE,连结BE,若AB=4,则BE的最小值为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线C1:y=mx2﹣2mx+m+4与y轴交于点A(0,3),与x轴交于点B、C(点B在点C左侧).
(1)求该抛物线的解析式;
(2)求点B的坐标;
(3)若抛物线C2:y=a(x﹣1)2﹣1(a≠0)与线段AB恰有一个公共点,结合函数的图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
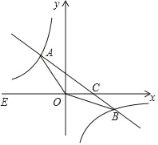
【题目】如图,在平面直角坐标系xOy的中,一次函数y=kx+b(k≠0)的图象与反比例函数y=![]() (m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n),线段OA=
(m≠0)的图象交于二、四象限内的A、B两点,与x轴交于C点,点B的坐标为(6,n),线段OA=![]() ,E为x轴上一点,且tan∠AOE=
,E为x轴上一点,且tan∠AOE=![]()
(1)求该反比例函数和一次函数的解析式;
(2)求△A0B的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
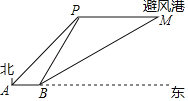
【题目】如图,一艘渔船正以60海里/小时的速度向正东方向航行,在A处测得岛礁P在东北方向上,继续航行1.5小时后到达B处,此时测得岛礁P在北偏东30°方向,同时测得岛礁P正东方向上的避风港M在北偏东60°方向.为了在台风到来之前用最短时间到达M处,渔船立刻加速以75海里/小时的速度继续航行_____小时即可到达.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】知识再现
如图1,若点![]() ,
,![]() 在直线
在直线![]() 同侧,
同侧,![]() ,
,![]() 到
到![]() 的距离分别是3和2,
的距离分别是3和2,![]() ,现在直线
,现在直线![]() 上找一点
上找一点![]() ,使
,使![]() 的值最小,做法如下:
的值最小,做法如下:
作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,连接
,连接![]() ,与直线
,与直线![]() 的交点就是所求的点
的交点就是所求的点![]() ,线段
,线段![]() 的长度即为
的长度即为![]() 的最小值,请你求出这个最小值.
的最小值,请你求出这个最小值.
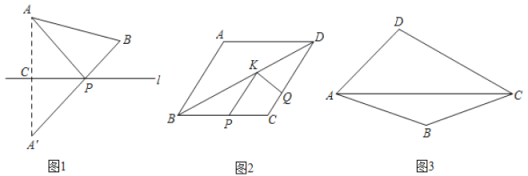
实践应用
如图2,菱形![]() 中
中![]() ,
,![]() ,点
,点![]() ,
,![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() ,
,![]() 上的任意一点,则
上的任意一点,则![]() 的最小值为______;
的最小值为______;
拓展延伸
如图3,在四边形![]() 的对角线
的对角线![]() 上找一点
上找一点![]() ,使
,使![]() ,保留作图痕迹,不必写出作法.
,保留作图痕迹,不必写出作法.
查看答案和解析>>
科目:初中数学 来源: 题型:
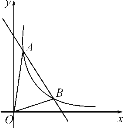
【题目】如图,一次函数y=kx+b与反比例函数y=![]() (x>0)的图象交于A(m,6),B(3,n)两点.
(x>0)的图象交于A(m,6),B(3,n)两点.
(1) 求一次函数的表达式;
(2) 根据图象写出kx+b-![]() <0的x的取值范围.
<0的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+mx+m﹣3=0.
(1)若该方程的一个根为2,求m的值及方程的另一个根;
(2)求证:不论m取何实数,该方程都有两个不相等的实数根.
查看答案和解析>>
科目:初中数学 来源: 题型:
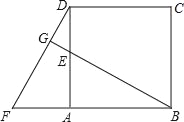
【题目】如图,已知四边形ABCD为正方形,点E是边AD上任意一点,△ABE接逆时针方向旋转一定角度后得到△ADF,延长BE交DF于点G,且AF=4,AB=7.
(1)请指出旋转中心和旋转角度;
(2)求BE的长;
(3)试猜测BG与DF的位置关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com