
【题目】如图,某水渠的横断面是等腰梯形,已知其斜坡AD和BC的坡度为1:0.6,现测得放水前的水面宽EF为1.2米,当水闸放水后,水渠内水面宽GH为2.1米 . 求放水后水面上升的高度是( )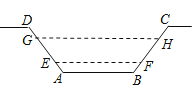
A.0.55
B.0.8
C.0.6
D.0.75
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】(1)观察推理:如图 1,△ABC 中,∠ACB=90°,AC=BC,直线 L 过点C,点 A,B 在直线 L 同侧,BD⊥L, AE⊥L,垂足分别为D,E
求证:△AEC≌△CDB
(2)类比探究:如图 2,Rt△ABC 中,∠ACB=90°,AC=4,将斜边 AB 绕点 A 逆时针旋转 90°至 AB’, 连接B’C,求△AB’C 的面积
(3)拓展提升:如图 3,等边△EBC 中,EC=BC=3cm,点 O 在 BC 上且 OC=2cm,动点 P 从点 E 沿射线EC 以 1cm/s 速度运动,连接 OP,将线段 OP 绕点O 逆时针旋转 120°得到线段 OF,设点 P 运动的时间为t 秒。
当t= 秒时,OF∥ED

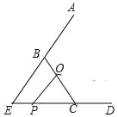
若要使点F 恰好落在射线EB 上,求点P 运动的时间t
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题的逆命题不成立的是( )
A. 如果两个数互为相反数,那么它们的和等于0
B. 如果两个角相等,那么这两个角的补角也相等
C. 如果两个数相等,那么它们的平方相等
D. 如果|a|=|b|,那么a=b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课外兴趣小组的同学们要测量被池塘相隔的两棵树A.B的距离,他们设计了如图所示的测量方案:从树A沿着垂直于AB的方向走到E , 再从E沿着垂直于AE的方向走到F , C为AE上一点,其中3位同学分别测得三组数据:①AC , ∠ACB;②EF.DE.AD;③CD , ∠ACB , ∠ADB.其中能根据所测数据求得A.B两树距离的有( )
A.0组
B.一组
C.二组
D.三组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,航行半小时后到达B处,此时观测到灯塔M在北偏东30°方向上,那么该船继续航行到达离灯塔距离最近的位置所需时间是( )
A.10分钟
B.15分钟
C.20分钟
D.25分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示,将直尺摆放在三角板上,使直尺与三角板的边分别交于点D , E , F , G , 已知∠CGD=42°
(1)求∠CEF的度数;
(2)将直尺向下平移,使直尺的边缘通过三角板的顶点B , 交AC边于点H , 如图②所示,点H , B在直尺上的度数分别为4,13.4,求BC的长(结果保留两位小数).(参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com