
【题目】下列命题的逆命题不成立的是( )
A. 如果两个数互为相反数,那么它们的和等于0
B. 如果两个角相等,那么这两个角的补角也相等
C. 如果两个数相等,那么它们的平方相等
D. 如果|a|=|b|,那么a=b
【答案】C
【解析】
首先理解逆命题的含义:一般的,在数学中把用语言、符号或式子表达的,可以判断真假的陈述句叫做命题。对于两个命题,如果一个命题的条件和结论分别是另外一个命题的结论和条件,那么这两个命题叫做互逆命题,其中一个命题叫做原命题,另外一个命题叫做原命题的逆命题。根据原命题写出各个命题的逆命题,再进一步判断真假.
A选项:逆命题是如果两个数的和是0,那么这两个数互为相反数,本选项正确;
B选项:逆命题是如果两个角的补角相等,那么这两个角相等,本选项正确;
C选项:逆命题是如果两个数的平方相等,这两个数相等,我们可以举个例子说明,![]() ,但
,但 ![]() ,正确的是这两个数也相等或互为相反数,本选项错误;
,正确的是这两个数也相等或互为相反数,本选项错误;
D选项:逆命题是如果a=b,那么|a|=|b|,本选项正确;
故选:C.


科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于(﹣2,0)和(4,0)两点,当函数值y>0时,自变量x的取值范围是( ) 
A.x<﹣2
B.x>4
C.﹣2<x<4
D.x>0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列一段文字,然后回答下列问题:
已知平面内两点M(x1,y1)、N(x2,y2),则这两点间的距离可用下列公式计算
MN=![]() .
.
例如:已知P(3,1)、Q(1,-2),则这两点的距离PQ=![]() .特别地,如果两点M(x1,y1)、N(x2,y2)所在的直线与坐标轴重合或平行于坐标轴或垂直于坐标轴,那么这两点间的距离公式可简化为MN=|x1-x2|或|y1-y2|.
.特别地,如果两点M(x1,y1)、N(x2,y2)所在的直线与坐标轴重合或平行于坐标轴或垂直于坐标轴,那么这两点间的距离公式可简化为MN=|x1-x2|或|y1-y2|.
(1)已知A(1,2)、B(-2,-3),试求A、B两点间的距离;
(2)已知A、B在平行于y轴的同一条直线上,点A的纵坐标为5,点B的纵坐标为-1,试求A、B两点间的距离;
(3)已知△ABC的顶点坐标分别为A(0,4)、B(-1,2)、C(4,2),你能判定△ABC的形状吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,己知△ABC , 任取一点O , 连AO , BO , CO , 并取它们的中点D , E , F , 得△DEF , 则下列说法正确的个数是( ) 
①△ABC与△DEF是位似图形; ②△ABC与△DEF是相似图形;
③△ABC与△DEF的周长比为1:2;④△ABC与△DEF的面积比为4:1.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,E是AB的中点,连接DE并延长交CB的延长线于点F,点G在边BC上,且∠GDF=∠ADF.

(1)求证:△ADE≌△BFE;
(2)连接EG,判断EG与DF的位置关系并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景
在△ABC中,AB,BC,AC的长分别为![]() ,
,![]() ,
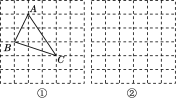
,![]() ,求这个三角形的面积.晓辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点三角形ABC(即△ABC的三个顶点都在小正方形的顶点处),如图①所示,这样不需求△ABC的高,而借用网格就能计算出它的面积.
,求这个三角形的面积.晓辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点三角形ABC(即△ABC的三个顶点都在小正方形的顶点处),如图①所示,这样不需求△ABC的高,而借用网格就能计算出它的面积.
(1)请你直接写出△ABC的面积:________.
(2)我们把上述求△ABC面积的方法叫做构图法.若△ABC的三边长分别为![]() a,2
a,2![]() a,
a,![]() a(a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.
a(a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.
探索创新
(3)若△ABC的三边长分别为![]() ,
,![]() ,2
,2![]() (m>0,n>0,且m≠n),试运用构图法(自己重新设计一个符合结构特征的网格)求出这个三角形的面积.
(m>0,n>0,且m≠n),试运用构图法(自己重新设计一个符合结构特征的网格)求出这个三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某水渠的横断面是等腰梯形,已知其斜坡AD和BC的坡度为1:0.6,现测得放水前的水面宽EF为1.2米,当水闸放水后,水渠内水面宽GH为2.1米 . 求放水后水面上升的高度是( )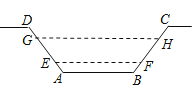
A.0.55
B.0.8
C.0.6
D.0.75
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=Rt∠,AC=8cm,BC=6cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒2cm,设运动的时间为t秒。

(1)当t为何值时,CP把△ABC的周长分成相等的两部分。
(2)当t为何值时,CP把△ABC的面积分成相等的两部分,并求出此时CP的长;
(3)当t为何值时,△BCP为等腰三角形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com