Question

【题目】等腰三角形中，两腰和底的长分别是10和13，求三角形的三个内角的度数（精确到1′） ．

Answer 1

【答案】解：如图所示，AB=AC=10，BC=13，AD是底边上的高，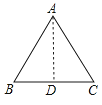

∵AD是底边上的高，
∴AD⊥BC ，
又∵AB=AC ，
∴BD=CD=6.5，∠BAD=∠CAD= ∠BAC ，
在Rt△ABD中，sin∠BAD= =0.65，
∴∠BAD≈40°32′，
∴∠BAC≈2∠BAD≈81°4′，∠B=∠C≈49°28′ ．
故△ABC的三个内角分别为：81°4′，49°28′，49°28′ ．
【解析】先画图，AB=AC=10，BC=13，AD是底边上的高，利用等腰三角形三线合一定理可知BD=CD=6.5，∠BAD=∠CAD= ∠BAC ， 在Rt△ABD中，利用∠BAD的正弦值的计算，结合计算器，可求∠BAD ， 从而可求∠B、∠BAC ， 那么∠C=∠B即可求 ．