
【题目】如图,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,航行半小时后到达B处,此时观测到灯塔M在北偏东30°方向上,那么该船继续航行到达离灯塔距离最近的位置所需时间是( )
A.10分钟
B.15分钟
C.20分钟
D.25分钟
科目:初中数学 来源: 题型:
【题目】(10分)如图,已知△ABC为等边三角形,点D、E分别在BC、AC边上,且AE=CD,AD与BE相交于点F。

(1)求证:△ABE≌△CAD;(2)求∠BFD的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,己知△ABC , 任取一点O , 连AO , BO , CO , 并取它们的中点D , E , F , 得△DEF , 则下列说法正确的个数是( ) 
①△ABC与△DEF是位似图形; ②△ABC与△DEF是相似图形;
③△ABC与△DEF的周长比为1:2;④△ABC与△DEF的面积比为4:1.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题背景
在△ABC中,AB,BC,AC的长分别为![]() ,
,![]() ,
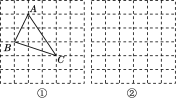
,![]() ,求这个三角形的面积.晓辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点三角形ABC(即△ABC的三个顶点都在小正方形的顶点处),如图①所示,这样不需求△ABC的高,而借用网格就能计算出它的面积.
,求这个三角形的面积.晓辉同学在解答这道题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出格点三角形ABC(即△ABC的三个顶点都在小正方形的顶点处),如图①所示,这样不需求△ABC的高,而借用网格就能计算出它的面积.
(1)请你直接写出△ABC的面积:________.
(2)我们把上述求△ABC面积的方法叫做构图法.若△ABC的三边长分别为![]() a,2
a,2![]() a,
a,![]() a(a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.
a(a>0),请利用图②的正方形网格(每个小正方形的边长为a)画出相应的△ABC,并求出它的面积.
探索创新
(3)若△ABC的三边长分别为![]() ,
,![]() ,2
,2![]() (m>0,n>0,且m≠n),试运用构图法(自己重新设计一个符合结构特征的网格)求出这个三角形的面积.
(m>0,n>0,且m≠n),试运用构图法(自己重新设计一个符合结构特征的网格)求出这个三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某水渠的横断面是等腰梯形,已知其斜坡AD和BC的坡度为1:0.6,现测得放水前的水面宽EF为1.2米,当水闸放水后,水渠内水面宽GH为2.1米 . 求放水后水面上升的高度是( )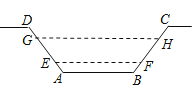
A.0.55
B.0.8
C.0.6
D.0.75
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D,E分别是边BC,AC上的点,且BD=EC,∠ADE=∠B.
(1)求证:AD=DE;
(2)若∠ADE=![]() ,求∠ADB的度数(用含x的代数式表示).
,求∠ADB的度数(用含x的代数式表示).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=∠C=36°,AB的垂直平分线交BC于点D,交AB于点H,AC的垂直平分线交BC于点E,交AC于点G,连接AD,AE,则下列结论错误的是( ) 
A.![]() =
= ![]()
B.AD,AE将∠BAC三等分
C.△ABE≌△ACD
D.S△ADH=S△CEG
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com