
【题目】如图,矩形ABCD的对角线AC.BD相交于点O , 过点O作OE⊥AC交AD于E , 若AB=6,AD=8,求sin∠OEA的值 . 
【答案】解:连接EC , 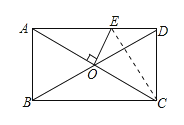
∵四边形ABCD为矩形,
∴OA=OC , ∠ABC=90°,
利用勾股定理得:AC= ![]() =10,即OA=5,
=10,即OA=5,
∵OE⊥AC ,
∴AE=CE ,
在Rt△EDC中,设EC=AE=x , 则有ED=AD-AE=8-x , DC=AB=6,
根据勾股定理得:x2=(8-x)2+62,
解得:x= ![]() ,
,
∴AE= ![]() ,
,
在Rt△AOE中,sin∠OEA= ![]() .
.
【解析】连接EC , 由四边形ABCD为矩形,得到对角线互相平分,即O为AC中点,再由OE垂直AC , 得到OE垂直平分AC , 即AE=CE , 在直角三角形EDC中,设EC=AE=x , 利用勾股定理列出关于x的方程,求出方程的解得到EC的长,即为AE的长,利用勾股定理求出AC的长,进而求出OA的长,在直角三角形AOE中,利用锐角三角函数定义即可求出sin∠OEA的值 .
【考点精析】通过灵活运用解直角三角形,掌握解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)即可以解答此题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD与四边形AEFG是位似图形,且AC:AF=2:3,则下列结论不正确的是( ) 
A.四边形ABCD与四边形AEFG是相似图形
B.AD与AE的比是2:3
C.四边形ABCD与四边形AEFG的周长比是2:3
D.四边形ABCD与四边形AEFG的面积比是4:9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,斜面AC的坡度(CD与AD的比)为1:2,AC=3 ![]() 米,坡顶有旗杆BC , 旗杆顶端B点与A点有一条彩带相连 . 若AB=10米,则旗杆BC的高度为( )
米,坡顶有旗杆BC , 旗杆顶端B点与A点有一条彩带相连 . 若AB=10米,则旗杆BC的高度为( )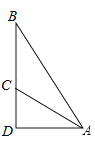
A.5米
B.6米
C.8米
D.(3+ ![]() )米
)米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,航行半小时后到达B处,此时观测到灯塔M在北偏东30°方向上,那么该船继续航行到达离灯塔距离最近的位置所需时间是( )
A.10分钟
B.15分钟
C.20分钟
D.25分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB , 坡面AC的倾斜角为45° . 为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i= ![]() :3 . 若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:
:3 . 若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)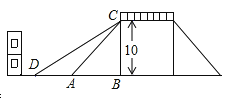
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=100°,BI、CI分别平分∠ABC,∠ACB,则∠BIC=________,若BM、CM分别平分∠ABC,∠ACB的外角平分线,则∠M=__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A,B,C,D,E,F是边长为1的正六边形的顶点,连接任意两点均可得到一条线段.在连接两点所得的所有线段中任取一条线段,取到长度为 ![]() 的线段的概率为( )
的线段的概率为( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com