
【题目】正方形ABCD中,E是AC上一点,EF⊥AB , EG⊥AD , AB=6,AE:EC=2:1.求四边形AFEG的面积.
【答案】解答:正方形ABCD中,∠DAB=90°,∠DAC=45°,
又∵∠AFE=∠AGE=90°,
∴四边形AFEG是矩形,∠AEG=90°-∠DAC=45°,
∴∠GAE=∠AEG=45°,
∴GE=AG ,
∴矩形AFEG是正方形,
∵四边形ABCD是正方形,
∴正方形AFEG∽正方形ABCD ,
∴ ![]() =(
=( ![]() )2=(
)2=( ![]() )2=
)2= ![]() ,
,
∴S正方形AFEG= ![]() S正方形AFEG=
S正方形AFEG= ![]() ×62=16.
×62=16.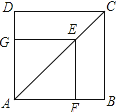
【解析】先证明四边形AFEG是正方形,再由相似的定义得出正方形AFEG∽正方形ABCD , 最后根据相似多边形的面积比等于相似比的平方进行求解.
【考点精析】掌握相似图形是解答本题的根本,需要知道形状相同,大小不一定相同(放大或缩小);判定:①平行;②两角相等;③两边对应成比例,夹角相等;④三边对应成比例.


科目:初中数学 来源: 题型:
【题目】如图,某水渠的横断面是等腰梯形,已知其斜坡AD和BC的坡度为1:0.6,现测得放水前的水面宽EF为1.2米,当水闸放水后,水渠内水面宽GH为2.1米 . 求放水后水面上升的高度是( )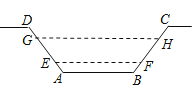
A.0.55
B.0.8
C.0.6
D.0.75
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在梯形ABCD中,AB∥DC , EF是梯形的中位线,AC交EF于G , BD交EF于H , 以下说法错误的是( ) 
A.AB∥EF
B.AB+DC=2EF
C.四边形AEFB和四边形ABCD相似
D.EG=FH
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠C=Rt∠,AC=8cm,BC=6cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒2cm,设运动的时间为t秒。

(1)当t为何值时,CP把△ABC的周长分成相等的两部分。
(2)当t为何值时,CP把△ABC的面积分成相等的两部分,并求出此时CP的长;
(3)当t为何值时,△BCP为等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=6cm , AC=12cm , 动点M从点A出发,以1cm∕秒的速度向点B运动,动点N从点C出发,以2cm∕秒的速度向点A运动,若两点同时运动,是否存在某一时刻t , 使得以点A、M、N为顶点的三角形与△ABC相似,若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=∠C=36°,AB的垂直平分线交BC于点D,交AB于点H,AC的垂直平分线交BC于点E,交AC于点G,连接AD,AE,则下列结论错误的是( ) 
A.![]() =
= ![]()
B.AD,AE将∠BAC三等分
C.△ABE≌△ACD
D.S△ADH=S△CEG
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=∠C=36°,AB的垂直平分线交BC于点D,交AB于点H,AC的垂直平分线交BC于点E,交AC于点G,连接AD,AE,则下列结论错误的是( ) 
A.![]() =
= ![]()
B.AD,AE将∠BAC三等分
C.△ABE≌△ACD
D.S△ADH=S△CEG
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,△ADF按顺时针方向旋转一定角度后得到△ABE,若AF=4.AB=7. 
(1)旋转中心为;旋转角度为;
(2)求DE的长度;
(3)指出BE与DF的关系如何?并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com