
【题目】如图,在△ABC中,AB=6cm , AC=12cm , 动点M从点A出发,以1cm∕秒的速度向点B运动,动点N从点C出发,以2cm∕秒的速度向点A运动,若两点同时运动,是否存在某一时刻t , 使得以点A、M、N为顶点的三角形与△ABC相似,若存在,求出t的值;若不存在,请说明理由.
【答案】解答:存在t=3秒或4.8秒,使以点A、M、N为顶点的三角形与△ABC相似(无此过程不扣分)
设经过t秒时,△AMN与△ABC相似,
此时,AM=t , CN=2t , AN=12-2t(0≤t≤6),
①当MN∥BC时,△AMN∽△ABC ,
则 ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得t=3;
②当∠AMN=∠C时,△ANM∽△ABC ,
则 ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
解得t=4.8;
故所求t的值为3秒或4.8秒.
【解析】首先设经过t秒时,△AMN与△ABC相似,可得AM=t , CN=2t , AN=12-2t(0≤t≤6),然后分别从当MN∥BC时,△AMN∽△ABC与当∠AMN=∠C时,△ANM∽△ABC去分析,根据相似三角形的对应边成比例即可求得答案.
【考点精析】解答此题的关键在于理解相似三角形的性质的相关知识,掌握对应角相等,对应边成比例的两个三角形叫做相似三角形.


科目:初中数学 来源: 题型:
【题目】数学课外兴趣小组的同学们要测量被池塘相隔的两棵树A.B的距离,他们设计了如图所示的测量方案:从树A沿着垂直于AB的方向走到E , 再从E沿着垂直于AE的方向走到F , C为AE上一点,其中3位同学分别测得三组数据:①AC , ∠ACB;②EF.DE.AD;③CD , ∠ACB , ∠ADB.其中能根据所测数据求得A.B两树距离的有( )
A.0组
B.一组
C.二组
D.三组
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标中,已知点O(0,0),A(0,2),B(1,0),点P是反比例函数y=- ![]()
图象上的一个动点,过点P作PQ⊥x轴,垂足为Q . 若以点O、P、Q为顶点的三角形与△OAB相似,则相应的点P共有( ).
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请按要求完成下面三道小题.
(1)如图1,AB=AC.这两条线段一定关于某条直线对称吗?如果是,请说明是哪条直线,并在图1中画出这条直线;如果不是,请说明理由.

(2)如图2,已知线段AB和点C.
求作线段CD,使它与AB成轴对称,且A与C是对称点,请画出图形,并简述画图过程.

(3)如图3,任意位置的两条线段AB,CD,AB=CD.你能通过对其中一条线段作有限次的轴对称使它们重合吗?如果能,请画出图形,并描述操作过程;如果不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,对称轴是直线x=﹣1,下列结论: ①abc<0;②2a+b=0;③a﹣b+c>0;④4a﹣2b+c<0
其中正确的是( )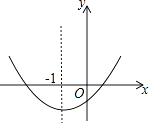
A.①②
B.只有①
C.③④
D.①④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=40°,以直角顶点C为旋转中心,将△ABC旋转到△A′B′C的位置,其中A′、B′分别是A、B的对应点,且点B在斜边A′B′上,直角边CA′交AB于D,则旋转角等于( ) 
A.70°
B.80°
C.60°
D.50°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com