
����Ŀ���밴Ҫ�������������С�⣮
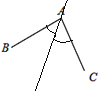
��1����ͼ1��AB=AC���������߶�һ������ij��ֱ�߶Գ�������ǣ���˵��������ֱ�ߣ�����ͼ1�л�������ֱ�ߣ�������ǣ���˵�����ɣ�

��2����ͼ2����֪�߶�AB�͵�C��
�����߶�CD��ʹ����AB����Գƣ���A��C�ǶԳƵ㣬�뻭��ͼ�Σ���������ͼ���̣�

��3����ͼ3������λ�õ������߶�AB��CD��AB=CD������ͨ��������һ���߶������ε���Գ�ʹ�����غ�������ܣ��뻭��ͼ�Σ��������������̣�������ܣ���˵�����ɣ�

���𰸡��������.
��������
��1������ABC��ƽ��������ֱ���ɣ���2��������AC�����߶�AC�Ĵ�ֱƽ���ߣ���Ϊ�Գ���b������B����ֱ��b�ĶԳƵ�D������CD��Ϊ����3������ȣ�2���IJ��軭ͼ��ͨ��һ����Գƣ�������ת��Ϊ��1�������������һ����ԳƼ�������������
��1����ͼ����ABC��ƽ��������ֱ���߶�BC�Ĵ�ֱƽ�����ǶԳ�����
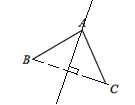
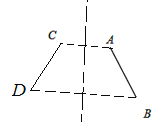
��2����ͼ��ʾ��
������AC�������߶�AC�Ĵ�ֱƽ����a����Ϊ�Գ��������B����ֱ��a�ĶԳƵ�D��
������CD������
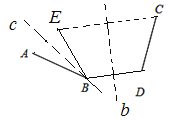
��3����ͼ��ʾ������BD�����߶�BD�Ĵ�ֱƽ����b������C����ֱ��b�ĶԳƵ�E������BE������ABE�Ľ�ƽ��������ֱ��c��������һ���߶���2�ε���ԳƼ�������һ���غϣ�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۹�����Ϋ�������ı�־�Խ�����Ϊ������߶ȣ���ͼ��һ�����ڸ���һ¥���ĵ�A�㴦�۲�۹�������C����������60�㣬Ȼ��������¥������B�㴦�۲�۹����ײ�D���ĸ�����30�� �� ��֪¥����ABԼ��45m �� �������Ϲ۲����ݿ���۹����ĸ�CD��m �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У�AD��BC �� E��F�ֱ���AB��CD���е㣬�����н��ۣ�
��EF��AD����S��ABO=S��DCO���ۡ�OGH�ǵ��������Σ���BG=DG����EG=HF ��
������ȷ�ĸ����ǣ�������
A.1��
B.2��
C.3��
D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У�AB=6cm �� AC=12cm �� ����M�ӵ�A��������1cm�M����ٶ����B�˶�������N�ӵ�C��������2cm�M����ٶ����A�˶���������ͬʱ�˶����Ƿ����ijһʱ��t �� ʹ���Ե�A��M��NΪ��������������ABC���ƣ������ڣ����t��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪BDΪ��ABC�Ľ�ƽ���ߣ��밴����Ҫ��������
��1������D��DE��BC��AB��E������A=68�㣬��AED=42��������BDC�Ķ���.
��2������ABC�Ľ�ƽ����CF��BD�ڵ�M,����A=60��������CMD�Ķ���.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���B=��C=36�㣬AB�Ĵ�ֱƽ���߽�BC�ڵ�D����AB�ڵ�H��AC�Ĵ�ֱƽ���߽�BC�ڵ�E����AC�ڵ�G������AD��AE�������н��۴�����ǣ� �� 
A.![]() =
= ![]()
B.AD��AE����BAC���ȷ�
C.��ABE�ա�ACD
D.S��ADH=S��CEG
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���ı���EFGH���ɾ���ABCD�����ƽ����Χ�ɵģ� ��֤���ı���EFGH�������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ��ֱ������ϵ�У���֪A��8��0������AOPΪ���������������Ϊ16������������P���У�������
A. 4�� B. 8�� C. 10�� D. 12��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η��̣�k��2��2x2+��2k+1��x+1=0����������ȵ�ʵ��������k��ȡֵ��Χ�ǣ� ��
A.k�� ![]() ��k��2
��k��2
B.k�� ![]() ��k��2
��k��2
C.k�� ![]() ��k��2
��k��2
D.k�� ![]() ��k��2
��k��2
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com