
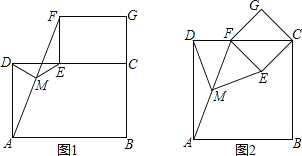
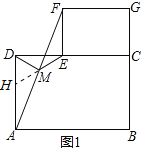
����Ŀ��������֤������ͼ1�ڷž���ֽƬABCD�����ֽƬECGF��ʹB��C��G������һ��ֱ���ϣ�CE�ڱ�CD�ϣ�����AF����MΪAF���е㣬����DM��ME���Բ���DM��ME��������ϵ����֤����Ľ��ۣ�
��չ�����죺
��1��������������֤�����е�ֽƬ����������ֽƬABCD��������ֽƬECGF�������������䣬��DM��ME�Ĺ�ϵΪ ��
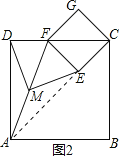
��2����ͼ2�ڷ�������ֽƬABCD��������ֽƬECGF��ʹ��F�ڱ�CD�ϣ���M��ΪAF���е㣬��֤����1���еĽ�����Ȼ������
���𰸡�DM=ME��֤�����̼���������1����DM=ME����2����DM=ME��֤�����̼�����.
��������
����������ӳ�EM��AD�ڵ�H������ABCD��CEFGΪ���εõ�AD��EF���õ���FME����AMHȫ�ȣ��õ�HM=EM������Rt��HDE�õ�HM=DE������Եõ��𰸣���1�����ӳ�EM��AD�ڵ�H������ABCD��CEFGΪ���εõ�AD��EF���õ���FME����AMHȫ�ȣ��õ�HM=EM������Rt��HDE�õ�HM=DE������Եõ��𰸣���2��������AE�����������ε����ʵó���FCE=45������FCA=45��������RT��ADF��AM=MF�ó�DM=AM=MF������RT��AEF��AM=MF�ó�AM=MF=ME���Ӷ�˵��DM=ME.
�����������ͼ1���ӳ�EM��AD�ڵ�H�����ı���ABCD��CEFG�Ǿ��Σ���AD��EF��
���EFM=��HAM��
���ߡ�FME=��AMH��FM=AM��
����FME����AMH��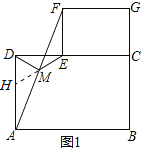
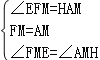
���FME�ա�AMH��ASA��
��HM=EM��
��RT��HDE��HM=DE��
��DM=HM=ME��
��DM=ME��
��1������ͼ1���ӳ�EM��AD�ڵ�H��
���ı���ABCD��CEFG�Ǿ��Σ�
��AD��EF��
���EFM=��HAM��
���ߡ�FME=��AMH��FM=AM��
����FME����AMH��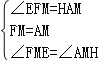
���FME�ա�AMH��ASA��
��HM=EM��
��RT��HDE��HM=EM
��DM=HM=ME��
��DM=ME��
��2������ͼ2������AE��
���ı���ABCD��ECGF�������Σ�
���FCE=45������FCA=45����
��AE��EC��ͬһ��ֱ���ϣ�
��RT��ADF��AM=MF��
��DM=AM=MF��
��RT��AEF��AM=MF��
��AM=MF=ME��
��DM=ME��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��ʾͬһʱ�̵ĺ�����ʱ��ͱ���ʱ�䣬����ʱ��Ϊ������
��1���豱��ʱ��Ϊx��ʱ������ʱ��Ϊy��ʱ��,��0��x��12����![]() ����
����![]() �ĺ�������ʽ������д�±���ͬһʱ�̵�����ʱ�䣩��
�ĺ�������ʽ������д�±���ͬһʱ�̵�����ʱ�䣩��
����ʱ�� | 7:30 | _____ | 2:50 |
��ʱ�� | ______ | 12:15 | ____ |
��2����ͼ2��ʾͬһʱ�̵�Ӣ����ʱ�䣨��ʱ�ƣ��ͱ���ʱ�䣬����ʱ��Ϊ��������������أ���ʱ�ƣ�ʱ��Ϊ7��30����ô��ʱ������ʱ���Ƕ��٣�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ĸ��㲻�ں���y=��2x+3��ͼ���� ( ��
A.��-5��13��B.��0.5��2��C.��3��0��D.��1��1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������ABC��һ��P,������PA=PB=PC,���P����ABC �� ��
A.������ƽ���ߵĽ���B.�������ߵĽ���C.�����ߵĽ���D.���ߴ�ֱƽ���ߵĽ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����x������������ô���и�ʽ��һ����ʾ�������ǣ� ��
A. 2017x B. x+2017 C. |2017x| D. |x|+2017
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������������ǣ����sin��=cos������ô������֮������Ĺ�ϵ�ǣ�������
A. ��=�� B. ��+��=90�� C. ��-��=90�� D. ��-��=90��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com