练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】老师在讲“实数”时画了一个图(如图)，即“以数轴的单位长度为边作一个正方形，然后以原点为圆心，正方形的对角线长为半径画弧交数轴于点A.

    (1)A点表示的数是多少?

    (2)请类比上面的作法在数轴上画出表示-的点B.(请保留作图痕迹)

    【答案】（1）-；（2）见解析

    【解析】

    （1）首先根据勾股定理求出正方形对角线的长度，即为OA的长，然后结合数轴的知识即可求解；

    （2）利用题中给出的方法画图，画图时即看是直角边和斜边分别多少，再从数轴上画出来即可解决问题．

    解：（1）∵12+12=2，

    ∴OA=，

    ∴A点表示的数是-；

    （2）如图以数轴的单位长度为边，作3×2的长方形，以数轴上的原点O为圆心，长方形的对角线的长为半径作弧与数轴负半轴交于一点B，则点B表示的数就是-．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】每到春夏交替时节，雌性杨树会以满天飞絮的方式来传播下一代，漫天飞舞的杨絮易引发皮肤病、呼吸道疾病等，给人们造成困扰，为了解市民对治理杨絮方法的赞同情况，某课题小组随机调查了部分市民（问卷调查表如表所示），并根据调查结果绘制了如下尚不完整的统计图．

    治理杨絮一一您选哪一项？（单选）

    A．减少杨树新增面积，控制杨树每年的栽种量

    B．调整树种结构，逐渐更换现有杨树

    C．选育无絮杨品种，并推广种植

    D．对雌性杨树注射生物干扰素，避免产生飞絮

    E．其他

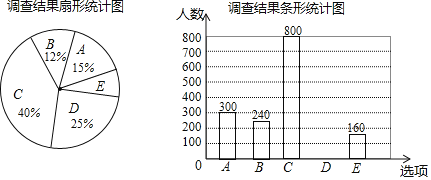
    根据以上统计图，解答下列问题：

    （1）本次接受调查的市民共有 　人；

    （2）扇形统计图中，扇形E的圆心角度数是　 　；

    （3）请补全条形统计图；

    （4）若该市约有90万人，请估计赞同“选育无絮杨品种，并推广种植”的人数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ACB=90°，∠A=60°，AB=6，△BCD为等边三角形，点E为△BCD围成的区域（包括各边）内的一点，过点E作EM∥AB，交直线AC于点M，作EN∥AC，交直线AB于点N，则的最大值为_____.

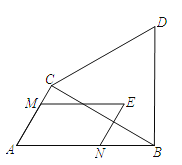
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图：、是锐角的两条高，、分别是、的中点，若EF=6，.

    （1）证明：；

    （2）判断与的位置关系，并证明你的结论；

    （3）求的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC中，∠A，∠B，∠C的对边分别是a，b，c，则满足下列条件的一定是直角三角形的是（　　）

    A. ∠A：∠B：∠C＝3：4：5B. a：b：c＝1：：3

    C. a＝7，b＝24，c＝25D. a＝32，b＝42，c＝52

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，把△ABC向上平移3个单位长度，再向右平移2个单位长度，得到△A′B′C′．

    ⑴写出A′、B′、C′的坐标；

    ⑵求出△ABC的面积；

    ⑶点P在y轴上，且△BCP与△ABC的面积相等，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，⊙P的圆心是（2，a）（a >0），半径是2，与y轴相切于点C，直线y=x被⊙P截得的弦AB的长为，则a的值是（ ）

    A. B. C. D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

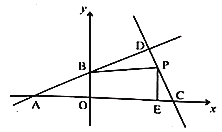
    【题目】如图，在平面直角坐标系中，直线与轴，轴的交点分别为，直线交轴于点，两条直线的交点为，点是线段上的一个动点，过点作轴，交轴于点，连接.

    求的面积；

    在线段上是否存在一点，使四边形为矩形，若存在，求出点坐标：若不存在，请说明理由；

    若四边形的面积为，设点的坐标为，求出关于的函数关系式，并写出自变量的取值范围.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠C＝90°，∠B＝30°，以点A为圆心，任意长为半径画弧分别交AB，AC于点M和N，再分别以点M，N为圆心，大于MN的长为半径画弧，两弧交于点P，连接AP并延长交BC于点D，则下列说法：①AD是∠BAC的平分线；②∠ADC＝60°；③点D在AB的垂直平分线上；④S△DAC：S△ABC＝1：3.其中正确的是__________________．(填所有正确说法的序号)

    查看答案和解析>>

    同步练习册答案