
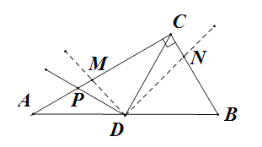
【题目】在Rt△ABC中,∠ACB=90°,∠B=60°.若点D为AB的中点,P为边AB上一点,且∠CDP=90°,将∠CDP绕点D顺时针方向旋转![]() (0°<
(0°<![]() <60°),角的两边分别与边AC、BC相交于M、N两点,则
<60°),角的两边分别与边AC、BC相交于M、N两点,则![]() =_______
=_______
【答案】![]()
【解析】
先根据直角三角形斜边上的中线性质得CD=AD=DB,则∠ACD=∠A=30°,∠BCD=∠B=60°,由于∠EDF=90°,可利用互余得∠CPD=60°,再根据旋转的性质得∠PDM=∠CDN=α,于是可判断△PDM∽△CDN,得到![]() ,然后在Rt△PCD中利用正切的定义得到tan∠PCD=tan30°=
,然后在Rt△PCD中利用正切的定义得到tan∠PCD=tan30°=![]() ,从而得到解.
,从而得到解.
∵点D为斜边AB的中点,
∴CD=AD=DB,
∴∠ACD=∠A=30°,∠BCD=∠B=60°,
∵∠EDF=90°,
∴∠CPD=60°,
∴∠MPD=∠NCD,
∵△EDF绕点D顺时针方向旋转α(0°<α<60°),
∴∠PDM=∠CDN=α,
∴△PDM∽△CDN,
∴![]() ,
,
在Rt△PCD中,∵tan∠PCD=tan30°=![]() ,
,
∴![]() .
.
故答案是:![]() .
.


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源: 题型:
【题目】为进一步发展基础教育,自2014年以来,某县加大了教育经费的投入,2014年该县投入教育经费6000万元。2016年投入教育经费8640万元。假设该县这两年投入教育经费的年平均增长率相同。
(1)求这两年该县投入教育经费的年平均增长率;
(2)若该县教育经费的投入还将保持相同的年平均增长率,请你预算2017年该县投入教育经费多少万元。
查看答案和解析>>
科目:初中数学 来源: 题型:
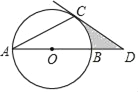
【题目】如图,AB是圆O的直径,AC是圆O的弦,过点C的切线交AB的延长线于点D,若∠A=∠D,CD=2![]() .
.
(1)求∠A的度数.
(2)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校冬季趣味运动会开设了“抢收抢种”项目,八(5)班甲、乙两个小组都想代表班级参赛,为了选择一个比较好的队伍,八(5)班的班委组织了一次选拔赛,甲、乙两组各10人的比赛成绩如下表:
甲组 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙组 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲组成绩的中位数是 分,乙组成绩的众数是 分.
(2)计算乙组的平均成绩和方差.
(3)已知甲组成绩的方差是1.4,则选择 组代表八(5)班参加学校比赛.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC.
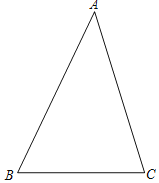
(1)请用尺规作图作出AC的垂直平分线,垂足为点D,交AB于点E(保留作图痕迹,不要求写作法).
(2)连接CE,如果△ABC的周长为32,DC的长为6,求△BCE的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料,并解答问题.
材料:将分式![]() 拆分成一个整式与一个分式(分子为整数)的和的形式.
拆分成一个整式与一个分式(分子为整数)的和的形式.
解:由分母为﹣x2+1,可设﹣x4﹣x2+3=(﹣x2+1)(x2+a)+b则﹣x4﹣x2+3=(﹣x2+1)(x2+a)+b=﹣x4﹣ax2+x2+a+b=﹣x4﹣(a﹣1)x2+(a+b)
∵对应任意x,上述等式均成立,∴![]() ,∴a=2,b=1
,∴a=2,b=1
∴![]() =
=![]() =
=![]() +
+![]() =x2+2+
=x2+2+![]() 这样,分式
这样,分式![]() 被拆分成了一个整式x2+2与一个分式
被拆分成了一个整式x2+2与一个分式![]() 的和.
的和.
解答:
(1)将分式![]() 拆分成一个整式与一个分式(分子为整数)的和的形式.
拆分成一个整式与一个分式(分子为整数)的和的形式.
(2)试说明![]() 的最小值为8.
的最小值为8.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则DF的长等于( )
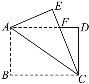
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
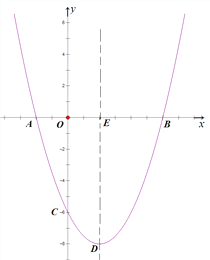
【题目】(题文)如图,抛物线![]() 与x轴交于A、B两点,与y轴交于点C,其对称轴交抛物线于点D,交x轴于点E,已知OB=OC=6.
与x轴交于A、B两点,与y轴交于点C,其对称轴交抛物线于点D,交x轴于点E,已知OB=OC=6.
(1)求抛物线的解析式及点D的坐标;
(2)连接BD,F为抛物线上一动点,当∠FAB=∠EDB时,求点F的坐标;
(3)平行于x轴的直线交抛物线于M、N两点,以线段MN为对角线作菱形MPNQ,当点P在x轴上,且PQ=![]() MN时,求菱形对角线MN的长.
MN时,求菱形对角线MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ABC=90°,AB=BC,直线l1、l2、l3分别通过A、B、C三点,且l1∥l2∥l3.若l1与l2的距离为5,l2与l3的距离为7,则Rt△ABC的面积为___________

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com