
【题目】如图,正方形ABCD的边长为4,点P在DC边上且DP=1,点Q是AC上一动点,则DQ+PQ的最小值为 . 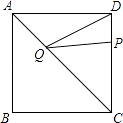
【答案】5
【解析】解:如图,连接BP, 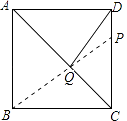
∵点B和点D关于直线AC对称,
∴QB=QD,
则BP就是DQ+PQ的最小值,
∵正方形ABCD的边长是4,DP=1,
∴CP=3,
∴BP= ![]() =5,
=5,
∴DQ+PQ的最小值是5.
所以答案是:5.
【考点精析】利用正方形的性质和轴对称-最短路线问题对题目进行判断即可得到答案,需要熟知正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形;已知起点结点,求最短路径;与确定起点相反,已知终点结点,求最短路径;已知起点和终点,求两结点之间的最短路径;求图中所有最短路径.


科目:初中数学 来源: 题型:
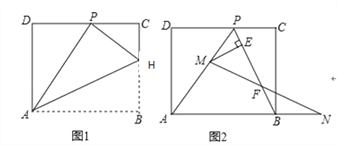
【题目】如图,将矩形ABCD沿AH折叠,使得顶点B落在CD边上的P点处.折痕与边BC交于点 H,
已知AD=8,HC:HB=3:5.
(1)求证:△HCP∽△PDA;
(2) 探究AB与HB之间的数量关系,并证明你的结论;
(3)连结BP,动点M在线段AP上(点M与点P、A不重合),动点N在线段AB的延长线上,且BN=PM,连结MN交PB于点F,作ME⊥BP于点E.试问当点M、N在移动过程中,线段EF的长度是否发生变化?若变化,说明理由;说明理由;若不变,求出线段EF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红每分钟踢毽子的次数正常范围为少于80次,但不少于50次,用不等式表示为( )
A. 50<x<80; B. 50≤x≤80; C. 50≤x<80; D. 50<x≤80;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解,我们把依次连接任意一个四边形各边中点得到的四边形叫中点四边形,如图1,在四边形ABCD中,E,F,G,H分别是边AB,BC,CD,DA的中点,依次连接各边中点得到中点四边形EFGH. 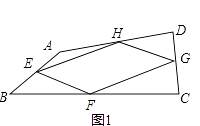
(1)这个中点四边形EFGH的形状是;
(2)如图2,在四边形ABCD中,点M在AB上且△AMD和△MCB为等边三角形,E、F、G、H分别为AB、BC、CD、AD的中点,试判断四边形EFGH的形状并证明. 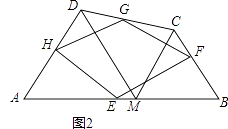
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列 ![]() 个命题:其中真命题是( ).
个命题:其中真命题是( ).
⑴三角形的外角和是 ![]() ;⑵三角形的三个内角中至少有两个锐角;⑶直角三角形两锐角互余;⑷相等的角是对顶角.
;⑵三角形的三个内角中至少有两个锐角;⑶直角三角形两锐角互余;⑷相等的角是对顶角.
A.( ![]() )(
)( ![]() )
)
B.( ![]() )(
)( ![]() )
)
C.( ![]() )(
)( ![]() )
)
D.( ![]() )(
)( ![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com