
����Ŀ����ͼ��������ABCD��AH�۵���ʹ�ö���B����CD���ϵ�P�㴦���ۺ����BC���ڵ� H,
��֪AD=8��HC:HB=3:5.
��1����֤����HCP�ס�PDA��
��2�� ̽��AB��HB֮���������ϵ����֤����Ľ��ۣ�
��3������BP������M���߶�AP�ϣ���M���P��A���غϣ�������N���߶�AB���ӳ����ϣ���BN=PM������MN��PB�ڵ�F����ME��BP�ڵ�E�����ʵ���M��N���ƶ������У��߶�EF�ij����Ƿ����仯�����仯��˵�����ɣ�˵�����ɣ������䣬����߶�EF�ij��ȣ�
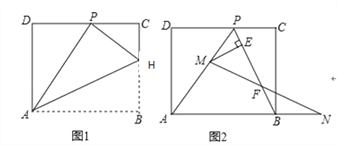
���𰸡���1��֤������������2��AB=2BH.�����ɼ�������(3) EF�ij��Ȳ��䣮
�������������������1���������Ƕ�Ӧ��ȵ������������ƿ���֤��
��2�����ݣ�1���Ľ��ۣ������������ε����ʿ��������֮��Ĺ�ϵ��
��3����MQ��AB��PB��Q���ɵ���MQP=��ABP�� Ȼ�����۵������ʿ�֪����APB=��ABP������MQP=��APB�����ݵȽǶԵȱ߿ɵ�MP=MQ����BN=PM�����ݵ��������ɵ�MQ=BN��Ȼ����ƽ���߷��߶γɱ�������EF=![]() PB�������ݹ��ɶ������.
PB�������ݹ��ɶ������.
�����������1�����۵������ʿ�֪��
��APH=��B=90�㣬 ���APD+��HPC=90�㣬
�֡�PHC+��HPC=90�㣬 ���APD=��PHC��
�֡�D=��C=90�㣬���HCP�ס�PDA��
��2��AB=2BH.
��HC:HB=3:5����HC=3x����HB=5x��
�ھ���ABCD�У�BC=AD=8 ����HC=3����HB=5
���۵������ʿ�֪HP=HB=5,AP=AB,
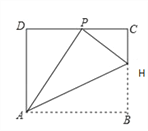
��Rt��HCP,��PC=4��
�ߡ�HCP�ס�PDA
��![]() ,��
,��![]()
��AB=AP=10=2BH,��AB=2BH.
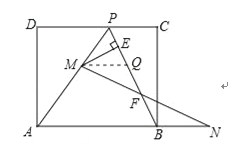
��3��EF�ij��Ȳ��䣮
��MQ��AB��PB��Q�� ���MQP=��ABP��
���۵������ʿ�֪����APB=��ABP��
���MQP=��APB��
��MP=MQ����BN=PM����MQ=BN��
��MQ��AB����![]() ��
��
��QF=FB��
��MP=MQ��ME��BP�� ��PE=QE����EF=![]() PB��
PB��
�ɣ�2���ã�PC=4��BC=8��
��PB=![]() =
=![]() ��
��
��EF=![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
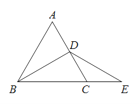
����Ŀ����ͼ����ABC�ǵȱ������Σ���D��AC���е㣬�ӳ�BC��E��ʹCE��CD.
(1)�ó߹���ͼ�ķ���������D��DM��BE������ΪM(��д������ֻ������ͼ�ۼ�)��
(2)��AB��2����EM�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У�E��AB��һ�㣬F��AD�ӳ�����һ�㣬��DF=BE�� 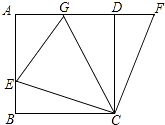
��1����֤��CE=CF��
��2������G��AD�ϣ��ҡ�GCE=45�㣬��GE=BE+GD������Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʦ��42��ѧ��ÿ������һ������Ʒ�������У�ÿ֧12Ԫ�ĸֱʣ�ÿ��4Ԫ��Բ�棬ÿ��16Ԫ�Ĵʵ䣬������216Ԫ�������ʦ���˸ֱ�֧���ʵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���x2��mx��2m2��0��
��1����֤������mΪ��ֵ���÷�����������ʵ������
��2����x��1�Ǹ÷��̵ĸ��������ʽ4m2+2m+5��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ĸ�������ƴ�ӳɵ�ͼ���У���A1��A2��A3������A10��ʮ��������������Ϊ���㣬�������������ֱ�������Σ� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���߳�Ϊ1cm��8��С������ƴ����ͼ��ʾ�ij�4cm����2cm�ij����Ρ�����Χ�ĸ���1�űൽ12�š��������A��B��C�ֱ�λ��4��8��12�Ÿ���ϣ�������ʱ�뷽��ͬʱ�ƶ�A��B��C���㣬ÿ�θ��ƶ�����һ����㣬����һ�ܻص�ԭ�ȵ�λ�ã�������У���ABC���γ�Ϊֱ�������Σ���ABC����������cm2��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�ı߳�Ϊ4����P��DC������DP=1����Q��AC��һ���㣬��DQ+PQ����СֵΪ �� 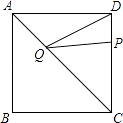
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com