
【题目】已知在平面直角坐标系中,A(a,0),B(0,b),D(0,c),其中a,b,c满足2a2+b2+c2-2ab-8a-2c+17=0,过坐标O作直线BC交线段OA于点C.
(1)如图1,当∠ODA=∠OCB时,求点C的坐标;

(2)如图2,在(1)条件下,过O作OE⊥BC交AB于点E,过E作EF⊥AD交OA于点N,交BC延长线于F,求证:BF=OE+EF;

【答案】(1)C(1,0);(2)见解析;
【解析】
(1)利用非负数的性质求出a,b,c的值,再证明△AOD≌△BOC(ASA),推出OC=OD=1解决问题;
(2)如图2中,设AD交BC于点Q,连接OQ,QE.想办法证明BQ=OE,FQ=EF即可解决问题;
(1)如图1中,
∵2a2+b2+c2-2ab-8a-2c+17=0,
∴(a-4)2+(a-b)2+(c-1)2=0,
∵(a-4)2≥0,(a-b)2≥0,(c-1)2≥0,
∴a=b=4,c=1,
∴A(4,0),B(0,4),D(0,1).
∴OB=OA,
∵∠ODA=∠OCB,∠AOD=∠BOC=90°,
∴△AOD≌△BOC(ASA),
∴OC=OD=1,
∴C(1,0).
(2)如图2中,设AD交BC于点Q,连接OQ,QE.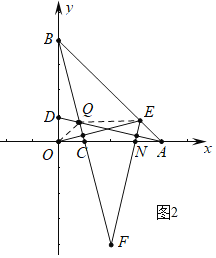
∵△AOD≌△BOC,
∴∠DAO=∠CBO,OD=OC,
∵OB=OA,
∴BD=AC,
∵∠AQB=∠CQA,
∴△DQB≌△CQA(AAS),
∴BQ=AQ,
∵OQ=OQ,OB=OA,BQ=AQ,
∴△OQB≌△OQA(SSS),
∴∠BOQ=∠AOQ=45°,
∴∠BOQ=∠OAE,
∵BF⊥OE,
∴∠OBC+∠BOE=90°,∠BOE+∠AOE=90°,
∴∠OBQ=∠AOE,∵OB=OA,
∴△OBQ≌△AOE(ASA),
∴BQ=OE,OQ=AE,
∵EQ=EQ,AQ=OE,OQ=AE,
∴△OEQ≌△AQE(SSS),
∴∠OEQ=∠AQE,
∵EF⊥AD,OE⊥BC,
∴∠F+∠FEO=90°,∠F+∠FQA=90°,
∴∠FEO=∠FQA,
∴∠FEQ=∠FQE,
∴EF=FQ,
∴BF=BQ+FQ=OE+EF.


 百年学典课时学练测系列答案
百年学典课时学练测系列答案科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为![]() ,连接AC、BD交于点O,CE平分∠ACD交BD于点E,
,连接AC、BD交于点O,CE平分∠ACD交BD于点E,
(1)求DE的长;
(2)过点EF作EF⊥CE,交AB于点F,求BF的长;
(3)过点E作EG⊥CE,交CD于点G,求DG的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知动点A在函数y=![]() (x>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC,直线DE分别交x轴,y轴于点P,Q,当QE:DP=9:25时,图中的阴影部分的面积等于___.
(x>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,延长CA至点D,使AD=AB,延长BA至点E,使AE=AC,直线DE分别交x轴,y轴于点P,Q,当QE:DP=9:25时,图中的阴影部分的面积等于___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点E,F,G分别是等边三角形ABC三边AB,BC,CA上的动点,且始终保持AE=BF=CG,设△EFG的面积为y,AE的长为x,y关于x的函数图象大致为图2所示,则等边三角形ABC的边长为___.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△ABC和△ADE中,AB=AC,AD=AE,且∠BAC=∠DAE.
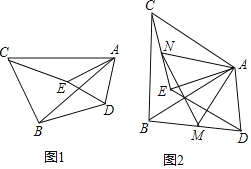
(1)求证:BD=CE;
(2)若点M,N分别是BD,CE的中点,如图2,连接AM,AN,MN,若AC=6,AE=4,∠EAC=60°,求AN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠B=30°,D为BC上一点,且∠DAB=45°.
(1) 求∠DAC的度数.
(2) 求证:△ACD是等腰三角形.
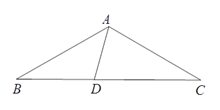
查看答案和解析>>
科目:初中数学 来源: 题型:
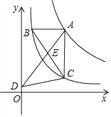
【题目】如图,点A是反比例函数y=![]() 图象上的任意一点,过点A作AB∥x轴,AC∥y轴,分别交反比例函数y=
图象上的任意一点,过点A作AB∥x轴,AC∥y轴,分别交反比例函数y=![]() 的图象于点B,C,连接BC,E是BC上一点,连接并延长AE交y轴于点D,连接CD,则S△DEC﹣S△BEA=_________.
的图象于点B,C,连接BC,E是BC上一点,连接并延长AE交y轴于点D,连接CD,则S△DEC﹣S△BEA=_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用若干个形状、大小完全相同的矩形纸片围成正方形,4个矩形纸片围成如图①所示的正方形,其阴影部分的面积为12;8个矩形纸片围成如图②所示的正方形,其阴影部分的面积为8;12个矩形纸片围成如图③所示的正方形,其阴影部分的面积为__.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com