
【题目】如图,E是正方形ABCD对角线BD上一点,EM⊥BC,EN⊥CD垂足分别是求M、N
(1)求证:AE=MN;
(2)若AE=2,∠DAE=30°,求正方形的边长.
【答案】
(1)
证明:连接EC.
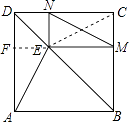
∵四边形ABCD是正方形,EM⊥BC,EN⊥CD,
∴∠NCM=∠CME=∠CNE=90°,
∴四边形EMCN为矩形.
∴MN=CE.
又∵BD为正方形ABCD的对角线,
∴∠ABE=∠CBE.
在△ABE和△CBE中
∵ 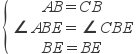 ,
,
∴△ABE≌△CBE(SAS).
∴AE=EC.
∴AE=MN.
(2)
解:过点E作EF⊥AD于点F,
∵AE=2,∠DAE=30°,
∴EF= ![]() AE=1,AF=AEcos30°=2×
AE=1,AF=AEcos30°=2× ![]() =
= ![]() .
.
∵BD是正方形ABCD的对角线,
∴∠EDF=45°,
∴DF=EF=1,
∴AD=AF+DF= ![]() +1,即正方形的边长为
+1,即正方形的边长为 ![]() +1.
+1.
【解析】(1)连接EC,根据题意可得出四边形EMCN为矩形,故MN=CE,再由SAS定理得出△ABE≌△CBE,进而可得出结论;(2)过点E作EF⊥AD,由直角三角形的性质可得出EF及AF的长,再由等腰直角三角形的性质得出DF的长,进而可得出结论.
【考点精析】利用正方形的性质对题目进行判断即可得到答案,需要熟知正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.


科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 过一点P只能作一条直线 B. 直线AB和直线BA表示同一条直线
C. 射线AB和射线BA表示同一条射线 D. 射线a比直线b短
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB=BC,对角线BD平分∠ABC,P是BD上一点,过点P作PM⊥AD,PN⊥CD,垂足分别为M,N.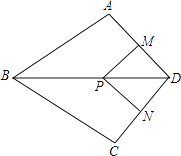
(1)求证:∠ADB=∠CDB;
(2)若∠ADC=90°,求证:四边形MPND是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果将抛物线y=x2+2向下平移1个单位,那么所得新抛物线的表达式是( )
A.y=(x﹣1)2+2
B.y=(x+1)2+2
C.y=x2+1
D.y=x2+3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】截止2019年3月8日,中国科幻电影《流浪地球》的票房约为45.6亿元,成为中国科幻电影的里程碑.其中45.6亿用科学记数法表示为( )
A. 4.56×108B. 45.6×108C. 4.56×109D. 0.456×1010
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式: ![]() =
= ![]() =1﹣
=1﹣ ![]() ,
, ![]() =
= ![]() =
= ![]() ﹣
﹣ ![]() ,
, ![]() =
= ![]() =
= ![]() ﹣
﹣ ![]() ,
, ![]() =
= ![]() =
= ![]() ﹣
﹣ ![]() ,…
,…
(1)由此可推导出 ![]() =;
=;
(2)猜想出能表示上述特点的一般规律,用含字母n的等式表示出来(n是正整数);
(3)请用(2)中的规律计算 ![]() +
+ ![]() +…+
+…+ ![]() 的结果.
的结果.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com