Question

【题目】如图，在四边形ABCD中，AB=BC，对角线BD平分∠ABC，P是BD上一点，过点P作PM⊥AD，PN⊥CD，垂足分别为M，N．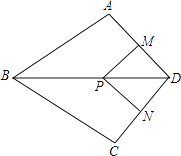

（1）求证：∠ADB=∠CDB；
（2）若∠ADC=90°，求证：四边形MPND是正方形．

Answer 1

【答案】
（1）

证明：∵对角线BD平分∠ABC，

∴∠ABD=∠CBD，

在△ABD和△CBD中，

，

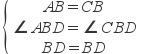∴△ABD≌△CBD（SAS），

∴∠ADB=∠CDB；

（2）

证明：∵PM⊥AD，PN⊥CD，

∴∠PMD=∠PND=90°，

∵∠ADC=90°，

∴四边形MPND是矩形，

∵∠ADB=∠CDB，

∴∠ADB=45°

∴PM=MD，

∴四边形MPND是正方形．

【解析】（1）根据角平分线的性质和全等三角形的判定方法证明△ABD≌△CBD，由全等三角形的性质即可得到：∠ADB=∠CDB；（2）若∠ADC=90°，由（1）中的条件可得四边形MPND是矩形，再根据两边相等的四边形是正方形即可证明四边形MPND是正方形．