
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌЖўДЮКЏЪ§y=ax2+bxЉ3ЕФЭМЯѓгыxжсНЛгкAЃЈЉ1ЃЌ0ЃЉЃЌЕуBЃЈ4ЃЌ0ЃЉЃЌгыyжсЕФНЛЕуЮЊC
ЃЈ1ЃЉЧѓЖўДЮКЏЪ§ЕФЙиЯЕЪНЃЛ
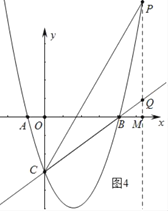
ЃЈ2ЃЉвбжЊЕуMЪЧЯпЖЮOBЩЯвЛЖЏЕуЃЌЙ§ЕуMзїЦНаагкyжсЕФжБЯпlЃЌжБЯпlгыХзЮяЯпНЛгкЕуEЃЌгыжБЯпBCНЛгкЕуFЃЌСЌНгCEЃЌШєЁїCEFгыЁїOBCЯрЫЦЃЌЧѓЕуMЕФзјБъЃЛ
ЃЈ3ЃЉвбжЊЕуMЪЧxжсе§АыжсЩЯвЛЖЏЕуЃЌЙ§ЕуMзїЦНаагкyжсЕФжБЯпlЃЌжБЯпlгыХзЮяЯпНЛгкPЃЌгыжБЯпBCНЛгкЕуQЃЌСЌНгCPЃЌНЋЁїCPQбиCPЗелКѓЃЌЪЧЗёДцдкетбљЕФжБЯпlЃЌЪЙЕУЗелКѓЕФЕуQИеКУТфдкyжсЩЯЃПШєДцдкЃЌЧыЧѓГіДЫЪБЕуMЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ

ЁОД№АИЁПЃЈ1ЃЉy=![]() x2Љ
x2Љ![]() xЉ3ЃЛЃЈ2ЃЉЕуMЕФзјБъЮЊЃЈ
xЉ3ЃЛЃЈ2ЃЉЕуMЕФзјБъЮЊЃЈ![]() ЃЌ0ЃЉЛђЃЈ3ЃЌ0ЃЉЃЛЃЈ3ЃЉЕуMЕФзјБъЮЊЃЈ
ЃЌ0ЃЉЛђЃЈ3ЃЌ0ЃЉЃЛЃЈ3ЃЉЕуMЕФзјБъЮЊЃЈ![]() ЃЌ0ЃЉЛђЃЈ
ЃЌ0ЃЉЛђЃЈ![]() ЃЌ0ЃЉЃЎ
ЃЌ0ЃЉЃЎ
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉРэгЩД§ЖЈЯЕЪ§ЗЈМДПЩНтОіЮЪЬтЃЛ
ЃЈ2ЃЉЗЈСНжжЧщаЮЂйШчЭМ1жаЃЌЕБCEЁЭCFЪБЃЌЁїCEFЁзЁїOBCЃЎЧѓГіжБЯпECЕФНтЮіЪНЃЌРћгУЗНГЬзщМДПЩНтОіЮЪЬтЃЛЂкШчЭМ2жаЃЌЕБCEЁЭEFЪБЃЌЁїEFCЁзЁїOBCЃЎДЫЪБEЃЈ3ЃЌЃ3ЃЉЃЌMЃЈ3ЃЌ0ЃЉЃЛ
ЃЈ3ЃЉЗжСНжжЧщаЮЃЎЂйШчЭМ3жаЃЌЕБЕуQЁфТфдкyжсЕФИКАыжсЩЯЪБЃЌЩшPЃЈmЃЌ ![]() m2Ѓ
m2Ѓ![]() mЃ3ЃЉЃЌдђQЃЈmЃЌ
mЃ3ЃЉЃЌдђQЃЈmЃЌ ![]() mЃ3ЃЉЃЎЂкШчЭМ4жаЃЌШчЭМ3жаЃЌЕБЕуQЁфТфдкyжсЕФИКАыжсЩЯЪБЃЌЩшPЃЈmЃЌ
mЃ3ЃЉЃЎЂкШчЭМ4жаЃЌШчЭМ3жаЃЌЕБЕуQЁфТфдкyжсЕФИКАыжсЩЯЪБЃЌЩшPЃЈmЃЌ ![]() m2Ѓ
m2Ѓ![]() mЃ3ЃЉЃЌдђQЃЈmЃЌ
mЃ3ЃЉЃЌдђQЃЈmЃЌ ![]() mЃ3ЃЉЃЎЭЌЗЈПЩЕУЃКPQЃНCQЃЎЗжБ№ЙЙНЈЗНГЬМДПЩНтОіЮЪЬтЃЎ
mЃ3ЃЉЃЎЭЌЗЈПЩЕУЃКPQЃНCQЃЎЗжБ№ЙЙНЈЗНГЬМДПЩНтОіЮЪЬтЃЎ
ЪдЬтНтЮіЃК
НтЃКЃЈ1ЃЉАбAЃЈЉ1ЃЌ0ЃЉЃЌЕуBЃЈ4ЃЌ0ЃЉДњШыyЃНax2ЃЋbxЉ3ЃЌ
ЕУЕН![]() ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊyЃН![]() x2Ѓ
x2Ѓ![]() xЃ3ЃЎ
xЃ3ЃЎ
ЃЈ2ЃЉЂйШчЭМ1жаЃЌЕБCEЁЭCFЪБЃЌЁїCEFЁзЁїOBCЃЎ

ЁпBЃЈ4ЃЌ0ЃЉЃЌCЃЈ0ЃЌЉ3ЃЉЃЌ
ЁржБЯпBCЕФНтЮіЪНЮЊyЃН![]() xЉ3ЃЌ
xЉ3ЃЌ
ЁржБЯпCEЕФНтЮіЪНЮЊyЃНЉ![]() xЉ3ЃЌ
xЉ3ЃЌ
гЩ ЃЌНтЕУ
ЃЌНтЕУ![]() Лђ
Лђ ЃЌ
ЃЌ
ЁрЕуEзјБъЮЊЃЈ![]() ЃЌЉ
ЃЌЉ![]() ЃЉЃЌMЃЈ
ЃЉЃЌMЃЈ![]() ЃЌ0ЃЉЃЛ
ЃЌ0ЃЉЃЛ
ЂкШчЭМ2жаЃЌЕБCEЁЭEFЪБЃЌЁїEFCЁзЁїOBCЃЎДЫЪБEЃЈ3ЃЌЉ3ЃЉЃЌMЃЈ3ЃЌ0ЃЉ

злЩЯЫљЪіЃЌТњзуЬѕМўЕФЕуMЕФзјБъЮЊЃЈ![]() ЃЌ0ЃЉЛђЃЈ3ЃЌ0ЃЉЃЛ
ЃЌ0ЃЉЛђЃЈ3ЃЌ0ЃЉЃЛ
ЃЈ3ЃЉДцдкЃЎЂйШчЭМ3жаЃЌЕБЕуQЁфТфдкyжсЕФИКАыжсЩЯЪБЃЌЩшPЃЈmЃЌ ![]() m2Ѓ
m2Ѓ![]() mЃ3ЃЉЃЌдђQЃЈmЃЌ
mЃ3ЃЉЃЌдђQЃЈmЃЌ ![]() mЉ3ЃЉЃЎ
mЉ3ЃЉЃЎ

ЁпPQЁЮCQЁфЃЌ
ЁрЁЯPCQЃНЁЯPCQЁфЃНЁЯCPQЃЌ
ЁрQCЃНQPЃНЉ![]() m2ЃЋ3mЃЌ
m2ЃЋ3mЃЌ
ЁпQMЁЮOCЃЌ
Ёр![]() ЃН
ЃН![]() ЃЌ
ЃЌ
Ёр ЃН
ЃН ЃЌ
ЃЌ
НтЕУmЃН![]() Лђ0ЃЈЩсЦњЃЉЃЌ
Лђ0ЃЈЩсЦњЃЉЃЌ
ЁрMЃЈ![]() ЃЌ0ЃЉЃЛ
ЃЌ0ЃЉЃЛ
ЂкШчЭМ4жаЃЌШчЭМ3жаЃЌЕБЕуQЁфТфдкyжсЕФИКАыжсЩЯЪБЃЌЩшPЃЈmЃЌ ![]() m2Ѓ
m2Ѓ![]() mЃ3ЃЉЃЌдђQЃЈmЃЌ
mЃ3ЃЉЃЌдђQЃЈmЃЌ ![]() mЉ3ЃЉЃЎЭЌЗЈПЩЕУЃКPQЃНCQЃЎ
mЉ3ЃЉЃЎЭЌЗЈПЩЕУЃКPQЃНCQЃЎ
 4
4
ЁпPQЁЮCQЁфЃЌ
ЁрЁЯPCQЃНЁЯPCQЁфЃНЁЯCPQЃЌ
ЁрQCЃНQPЃНЉ![]() m2ЃЋ3mЃЌ
m2ЃЋ3mЃЌ
ЁпQMЁЮOCЃЌ
Ёр![]() ЃН
ЃН![]() ЃЌ
ЃЌ
Ёр![]() ЃН
ЃН ЃЌ
ЃЌ
НтЕУmЃН![]() Лђ0ЃЈЩсЦњЃЉЃЌ
Лђ0ЃЈЩсЦњЃЉЃЌ
ЁрMЃЈ![]() ЃЌ0ЃЉЃЌ
ЃЌ0ЃЉЃЌ
злЩЯЫљЪіЃЌТњзуЬѕМўЕФЕуMЕФзјБъЮЊЃЈ![]() ЃЌ0ЃЉЛђЃЈ
ЃЌ0ЃЉЛђЃЈ![]() ЃЌ0ЃЉЃЎ
ЃЌ0ЃЉЃЎ


 ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ
ЬьЬьЯђЩЯвЛБОКУОэЯЕСаД№АИ аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ
аЁбЇЩњ10ЗжжггІгУЬтЯЕСаД№АИ ФПБъВтЪдЯЕСаД№АИ
ФПБъВтЪдЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПБОбЇЦкЃЌДѓаЫЧјПЊеЙСЫЁАЧЁЭЌбЇЩйФъЃЌЦЗЪЋДЪУРдЯЁБжаЛЊДЋЭГЪЋДЪДѓШќЛюЖЏ![]() аЁНЭГМЦСЫАрМЖ30УћЭЌбЇЫФдТЗнЕФЪЋДЪБГЫаЪ§СПЃЌОпЬхЪ§ОнШчБэЫљЪОЃК
аЁНЭГМЦСЫАрМЖ30УћЭЌбЇЫФдТЗнЕФЪЋДЪБГЫаЪ§СПЃЌОпЬхЪ§ОнШчБэЫљЪОЃК
ЪЋДЪЪ§СП | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
ШЫЪ§ | 3 | 4 | 4 | 5 | 7 | 5 | 1 | 1 |
ФЧУДет30УћЭЌбЇЫФдТЗнЪЋДЪБГЫаЪ§СПЕФжкЪ§КЭжаЮЛЪ§ЗжБ№ЪЧ![]() ЁЁЁЁ
ЁЁЁЁ![]()
A. 11ЃЌ7 B. 7ЃЌ5 C. 8ЃЌ8 D. 8ЃЌ7
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
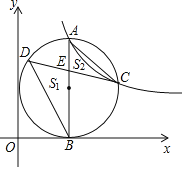
ЁОЬтФПЁПШчЭМЃЌЕуAЪЧЗДБШР§КЏЪ§![]() ЭМЯѓЕквЛЯѓЯоЩЯвЛЕуЃЌЙ§ЕуAзї
ЭМЯѓЕквЛЯѓЯоЩЯвЛЕуЃЌЙ§ЕуAзї![]() жсгкBЕуЃЌвдABЮЊжБОЖЕФдВЧЁКУгыyжсЯрЧаЃЌНЛЗДБШР§КЏЪ§ЭМЯѓгкЕуCЃЌдкABЕФзѓВрАыдВЩЯгавЛЖЏЕуDЃЌСЌНсCDНЛABгкЕу
жсгкBЕуЃЌвдABЮЊжБОЖЕФдВЧЁКУгыyжсЯрЧаЃЌНЛЗДБШР§КЏЪ§ЭМЯѓгкЕуCЃЌдкABЕФзѓВрАыдВЩЯгавЛЖЏЕуDЃЌСЌНсCDНЛABгкЕу![]() МЧ
МЧ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌ
ЃЌ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌСЌНгBCЃЌдђ
ЃЌСЌНгBCЃЌдђ![]() ЪЧ______Ш§НЧаЮЃЌШє
ЪЧ______Ш§НЧаЮЃЌШє![]() ЕФжЕзюДѓЮЊ1ЃЌдђkЕФжЕЮЊ______ЃЎ
ЕФжЕзюДѓЮЊ1ЃЌдђkЕФжЕЮЊ______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() ЪЧжБЯп
ЪЧжБЯп![]() ЩЯвЛЕуЃЌ
ЩЯвЛЕуЃЌ![]() ЮЊШЮвЛЩфЯпЃЌ
ЮЊШЮвЛЩфЯпЃЌ![]() ЦНЗж
ЦНЗж![]() ЃЌ
ЃЌ![]() ЦНЗж
ЦНЗж![]() ЃЌ
ЃЌ

ЃЈ1ЃЉЗжБ№аДГіЭМжа![]() гы
гы![]() ЕФВЙНЧЃЛ
ЕФВЙНЧЃЛ
ЃЈ2ЃЉ![]() гы
гы![]() гадѕбљЕФЪ§СПЙиЯЕЃЌЧыЫЕУїРэгЩ.
гадѕбљЕФЪ§СПЙиЯЕЃЌЧыЫЕУїРэгЩ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙлВьЯТСаИїЪН
ЃЈxЉ1ЃЉЃЈx+1ЃЉЃНx2Љ1
ЃЈxЉ1ЃЉЃЈx2+x+1ЃЉЃНx3Љ1
ЃЈxЉ1ЃЉЃЈx3+x2+x+1ЃЉЃНx4Љ1
ЃЈ1ЃЉИљОнвдЩЯЙцТЩЃЌдђЃЈxЉ1ЃЉЃЈx6+x5+x4+x3+x2+x+1ЃЉЃНЁЁ ЁЁЃЛ
ЃЈ2ЃЉФуФмЗёгЩДЫЙщФЩГівЛАуЙцТЩЃЈxЉ1ЃЉЃЈxn+xnЉ1+ЁЁ+x+1ЃЉЃНЁЁ ЁЁЃЛ
ЃЈ3ЃЉИљОнвдЩЯЙцТЩЧѓ32018+32017+32016+Ё32+3+1ЕФНсЙћЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЮЊДђдьжЧЛлПЮЬУЃЌзМБИМЏЬхЙКТђвЛХњЦНАхЕчФдЃЌдМЦЛЎЖЉЙК60ЬЈЃЌУПЬЈ1000дЊЃЌЩЬМвБэЪОЃЌШчЙћЖрЙКЃЌПЩвдгХЛнЃЌНсЙћаЃГЄЪЕМЪЖЉЙКСЫ72ЬЈЃЌУПЬЈМѕМл30дЊЃЌЕЋЩЬМвЛёЕУЭЌбљЖрЕФРћШѓ.
ЃЈ1ЃЉЧѓУПЬЈЦНАхЕчФдЕФГЩБОЪЧЖрЩйдЊЃП
ЃЈ2ЃЉЧѓЩЬМвЕФРћШѓЪЧЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЪаЮЊСЫНтИпЗхЪБЖЮДгзмеОГЫ16ТЗГЕГіааЕФШЫЪ§ЃЌЫцЛњГщВщСЫ10ИіАрДЮГЫИУТЗГЕШЫЪ§ЃЌНсЙћШчЯТЃК
14ЃЌ23ЃЌ16ЃЌ25ЃЌ23ЃЌ28ЃЌ26ЃЌ27ЃЌ23ЃЌ25ЃЎ
ЃЈ1ЃЉМЦЫует10ИіАрДЮГЫГЕШЫЪ§ЕФЦНОљЪ§ЃЛ
ЃЈ2ЃЉШчЙћ16ТЗГЕдкИпЗхЪБЖЮДгзмеОЙВГіГЕ60ИіАрДЮЃЌИљОнЩЯУцЕФМЦЫуНсЙћЃЌЙРМЦдкИпЗхЪБЖЮДгзмеОГЫИУТЗГЕГіааЕФГЫПЭЙВгаЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЦНУцжБНЧзјБъЯЕжаЃЌЕуOЮЊзјБъдЕуЃЌОиаЮOABCЕФБпOAЃЌOCдкзјБъжсЩЯЃЌЕуBЃЈ12ЃЌ4ЃЉЃЌЕуDЃЈ3ЃЌ0ЃЉЃЌЕуEЃЈ0ЃЌ2ЃЉЃЌЙ§ЕуDзїDFЁЭDEЃЌНЛABгкЕуFЃЌСЌНсEFЃЌНЋЁїDEFШЦЕуEФцЪБеыЗНЯђа§зЊЃЌа§зЊНЧЖШЮЊІШЃЈ0ЁуЃМІШЃМ180ЁуЃЉЃЎ
ЃЈ1ЃЉЧѓtanЁЯDFEЃЎ
ЃЈ2ЃЉдка§зЊЙ§ГЬжаЃЌЕБЁїDFEЕФвЛБпгыжБЯпABЦНааЪБЃЌЧѓжБЯпABНиЁїDFEЫљЕУЕФШ§НЧаЮЕФУцЛ§ЃЎ
ЃЈ3ЃЉдка§зЊЙ§ГЬжаЃЌЕБЁЯDFEЕФСНБпЫљдкжБЯпгыyжсЮЇГЩЕФШ§НЧаЮЮЊЕШбќШ§НЧаЮЪБЃЌЧѓЕуFЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙлВьЯТБэШ§ааЪ§ЕФЙцТЩЃЌЛиД№ЯТСаЮЪЬтЃК
Ек1Са | Ек2Са | Ек3Са | Ек4Са | Ек5Са | Ек6Са | Ё | |
Ек1аа | -2 | 4 | -8 | a | -32 | 64 | Ё |
Ек2аа | 0 | 6 | -6 | 18 | -30 | 66 | Ё |
Ек3аа | -1 | 2 | -4 | 8 | -16 | b | Ё |
ЃЈ1ЃЉЕк1ааЕФЕкЫФИіЪ§aЪЧ ЃЛЕк3ааЕФЕкСљИіЪ§bЪЧ ЃЛ
ЃЈ2ЃЉШєЕк1ааЕФФГвЛСаЕФЪ§ЮЊcЃЌдђЕк2аагыЫќЭЌвЛСаЕФЪ§ЮЊ ЃЛ
ЃЈ3ЃЉвбжЊЕкnСаЕФШ§ИіЪ§ЕФКЭЮЊ2562ЃЌШєЩшЕк1ааЕкnСаЕФЪ§ЮЊxЃЌЪдЧѓxЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com