Question

12．如图1、图2，一电线杆PA由另一圆柱体水泥杆BD作支撑，支撑杆有一日突然于E处折断（因有钢筋相连，两段水泥杆没有完全断开）．由于重力作用，下段下倾，上段下坠，造成支撑杆于E处下凹，并停止在图2的状态．折断下凹前、后的有关数据标注如图所示．问支撑杆折断后，它的顶端下落的竖直距离．（可使用科学计算器，精确到0.01m，sin63°≈0.89，cos63°≈0.45，tan63°≈1.96，$\sqrt{9.8176}$≈3.13，$\sqrt{2.73}$≈1.65）

Answer 1

分析 根据题意利用锐角三角函数关系得出BD，AD的长，进而在图2中求出AD的长，进而得出顶端下落的竖直距离．

解答 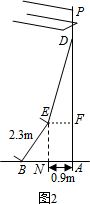解：如图1，∵∠DBA=63°，AB=2.5m，
∴tan63°=$\frac{AD}{AB}$=$\frac{AD}{2.5}$≈1.96，
解得：AD=4.9，
cos63°=$\frac{AB}{BD}$=$\frac{2.5}{BD}$≈0.45，
解得：BD≈5.56，
如图2，过点E作EF⊥AD于点F，
∵AB=2.5m，AN=0.9m，
∴BN=1.6m，EF=0.9m，
∴AF=EN=$\sqrt{B{E}^{2}-B{N}^{2}}$=$\sqrt{2.73}$≈1.65（m），
∵BD=5.56m，BE=2.3m，
∴DE=3.26m，
∴DF=$\sqrt{D{E}^{2}-E{F}^{2}}$=$\sqrt{9.8176}$≈3.13（m），
故AD=DF+AF=1.65+3.13=4.78（m），
故支撑杆折断后，它的顶端下落的竖直距离为：4.9-4.78=0.12（m）．

点评 此题主要考查了解直角三角形的应用，根据题意得出AD的变化长度是解题关键．