
【题目】已知直线![]() ,直线
,直线![]() 与
与![]() 、
、![]() 分别交于C、D两点,点P是直线
分别交于C、D两点,点P是直线![]() 上的一动点.
上的一动点.
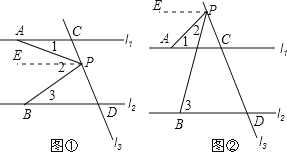
(1)如图,若动点P在线段CD之间运动(不与C、D两点重合),问在点P的运动过程中是否始终具有![]() 这一相等关系?试说明理由;
这一相等关系?试说明理由;
(2)如图,当动点P在线段CD之外且在![]() 的上方运动(不与C、D两点重合),则上述结论是否仍成立?若不成立,试写出新的结论,并说明理由;
的上方运动(不与C、D两点重合),则上述结论是否仍成立?若不成立,试写出新的结论,并说明理由;

【答案】(1)∠3+∠1=∠2成立.(2)∠3+∠1=∠2不成立,新的结论为∠3-∠1=∠2.
【解析】试题分析:(1)∠3+∠1=∠2成立,理由如下:过点P作PE∥![]() ,利用两直线平行内错角相等得到
,利用两直线平行内错角相等得到![]() 根据
根据![]() ∥
∥![]() ,得到PE∥
,得到PE∥![]() ,再利用两直线平行内错角相等,根据
,再利用两直线平行内错角相等,根据![]() 等量代换即可得证;
等量代换即可得证;
(2)∠3+∠1=∠2不成立,新的结论为∠3-∠1=∠2,理由为:过P作PE∥![]() ,同理得到
,同理得到![]() 根据
根据![]() 等量代换即可得证;
等量代换即可得证;
试题解析:(1)∠3+∠1=∠2成立,理由如下:
过点P作PE∥l1,
∴∠1=∠AEP,
∵l1∥l2,
∴PE∥l2,
∴∠3=∠BPE,
∵∠BPE+∠APE=∠2,
∴∠3+∠1=∠2;
(2)∠3+∠1=∠2不成立,新的结论为∠3∠1=∠2,理由为:
过P作PE∥l1,
∴∠1=∠APE,
∵l1∥l2,
∴PE∥l2,
∴∠3=∠BPE,
∵∠BPE∠APE=∠2,
∴∠3∠1=∠2.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
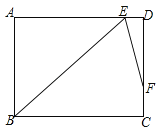
【题目】在矩形ABCD中,∠B的角平分线BE与AD交于点E,∠BED的角平分线EF与DC交于点F,若AB=9,DF=2FC,则BC=____.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司投资新建了一商场,共有商铺30间.据预测,当每间的年租金定为10万元时,可全部租出.每间的年租金每增加5 000元,少租出商铺1间.该公司要为租出的商铺每间每年交各种费用1万元,未租出的商铺每间每年交各种费用5 000元.
(1)当每间商铺的年租金定为13万元时,能租出多少间?
(2)当每间商铺的年租金定为多少万元时,该公司的年收益(收益=租金-各种费用)为284万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,新城区新建了三个商业城A,B,C,其中C在A的正东方向,在A处测得B在A的南偏东52°的方向,在C处测得B在C的南偏东26°的方向,已知A和B的距离是1000m.现有甲、乙两个工程对修建道路,甲修建一条从A到C的笔直道路AC,乙修建一条从B到直线AC最近的道路BD.求甲、乙修建的道路各是多长.(结果精确到1m)(参考数据:sin38°≈0.62,cos38°≈0.79,tan38°≈0.78,sin64°≈0.90,cos64°≈0.44,tan64°≈2.05)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,分析下列四个结论:①△AEF∽△CAB;②CF=2AF;③DF=DC;④tan∠CAD=![]() .其中正确的结论有( )
.其中正确的结论有( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】邻边不相等的平行四边形纸片,剪去一个菱形,余下一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又余下一个四边形,称为第二 次操作;……依此类推,若第n次操作余下的四边形是菱形,则称原平行四边形为n阶准菱形.如图1,平行四边形ABCD中,若AB=1,BC=2,则平行四 边形ABCD为1阶准菱形.

(I)判断与推理:
(i)邻边长分别为2和3的平行四边形是_________阶准菱形;
(ii)为了剪去一个菱形,进行如下操作:如图2,把平行四边形ABCD沿BE折叠(点E在AD上),使点A落在BC边上的点F,得到四边形ABFE,请证明四边形ABFE是菱形.

(Ⅱ)操作与计算:
已知平行四边形ABCD的邻边长分别为l,a(a>1),且是3阶准菱形,请画出平行四边形ABCD及裁剪线的示意图,并在图形下方写出a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列条件之一能使平行四边形ABCD是菱形的为_____________.
①AC⊥BD;②∠BAD=90°;③AB=BC;④AC=BD.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在三角形中,把一边的中点到这条边的高线的距离叫做这条边的中垂距.
例:如图①,在△ABC中,D为边BC的中点,AE⊥BC于E,则线段DE的长叫做边BC的中垂距.
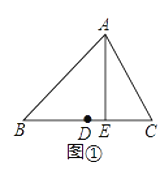
(1)设三角形一边的中垂距为d(d≥0).若d=0,则这样的三角形一定是________,推断的数学依据是________.
(2)如图②,在△ABC中,∠B=45°,AB=![]() ,BC=8,AD为边BC的中线,求边BC的中垂距.
,BC=8,AD为边BC的中线,求边BC的中垂距.

(3)如图③,在矩形ABCD中,AB=6,AD=4.点E为边CD的中点,连结AE并延长交BC的延长线于点F,连结AC.求△ACF中边AF的中垂距.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,它与x轴的两个交点分别为(﹣1,0),(3,0).对于下列命题:①b+2a=0;②abc>0;③a﹣2b+4c<0;④8a+c>0.其中正确的有( )个.
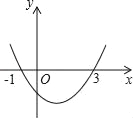
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com