
【题目】某企业为了提高工人劳动的积极性,决定对工人的月工资进行调整.已知该企业有 n 名工人,调整后的月工资 y(元)与调整前的月工资 x(元)满足一次函数关系,如下表:

(1)求 y 与 x 的函数关系式;
(2)若某名工人调整前月工资是4800元,那么调整后这名工人月工资增加了多少元?
(3)这 ![]() 名工人调整前、后的平均月工资分别为
名工人调整前、后的平均月工资分别为![]() ,
,![]() ,猜想
,猜想![]() 与
与![]() 的关系式,并写出推导过程.
的关系式,并写出推导过程.
【答案】(1)y=1.08x+100;(2)调整后这名工人月工资增加了484元;(3) ![]() .推导过程见解析.
.推导过程见解析.
【解析】
(1)由题干中调整后的月工资![]() (元)与调整前的月工资
(元)与调整前的月工资![]() (元)满足一次函数关系,直接设
(元)满足一次函数关系,直接设![]() .将表格中第二名、第三名工人调价前后的值分别代入即可求解;
.将表格中第二名、第三名工人调价前后的值分别代入即可求解;
(2)将![]() 4800代入(1)的结论计算即可;
4800代入(1)的结论计算即可;
(3)根据平均数的定义列式相加即可证明.
(1) ∵调整后的月工资![]() (元)与调整前的月工资
(元)与调整前的月工资![]() (元)满足一次函数关系,
(元)满足一次函数关系,
设y 与 x 的函数关系式为![]() .
.
依题意得:![]() ,
,
解得:![]() ,
,
∴y 与 x 的函数关系式为![]() ;
;
(2) 当![]() 时,
时,![]() (元),
(元),
∴5284-4800=484(元),
∴调整后这名工人月工资增加了484元;
(3) ∵![]()
![]()
![]()
![]()
![]() .
.


 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案科目:初中数学 来源: 题型:
【题目】(1)写出图1中函数图象的解析式![]() ;
;

(2)如图2,过直线![]() 上一点
上一点![]() 作
作![]() 轴的垂线交
轴的垂线交![]() 的图象于点
的图象于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
①试比较![]() 与
与![]() 的大小,并证明你的结论;
的大小,并证明你的结论;
②若![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
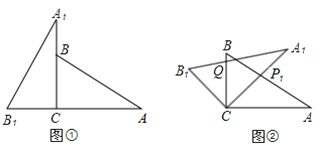
【题目】将两块全等的三角板如图①摆放,其中∠A1CB1=∠ACB=90°,∠A1=∠A=30°.
(1)将图①中的△A1B1C顺时针旋转45°得图②,点P1是A1C与AB的交点,点Q是A1B1与BC的交点,求证:CP1=CQ;
(2)在图②中,若AP1=2,则CQ等于多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,∠ABC=30°,△CDE是等边三角形,点D在边AB上.

(1)如图1,当点E在边BC上时,求证DE=EB;
(2)如图2,当点E在△ABC内部时,猜想ED和EB数量关系,并加以证明;
(3)如图3,当点E在△ABC外部时,EH⊥AB于点H,过点E作GE∥AB,交线段AC的延长线于点G,AG=5CG,BH=3.求CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
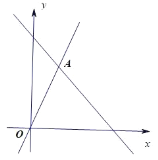
【题目】如图,一次函数 y=-x+6的图像与正比例函数 y=2x 的图像交于点 A.
(1)求点 A 的坐标;
(2)已知点 B 在直线 y=-x+6上,且横坐标为5,在 x 轴上确定点 P,使 PA+PB 的值最小,求出此时 P 点坐标,并直接写出 PA+PB 的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是等边
是等边![]() 内一点,
内一点, ![]() .将
.将![]() 绕点
绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 得
得![]() ,连接
,连接![]() .
.

(1)求证: ![]() 是等边三角形;
是等边三角形;
(2)当![]() 时,试判断
时,试判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)探究:当![]() 为多少度时,
为多少度时, ![]() 是等腰三角形?
是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
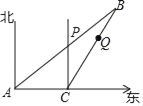
【题目】如图所示,甲、乙两船同时由港口A出发开往海岛B,甲船沿某一方向直航140海里的海岛B,其速度为14海里/小时;乙船速度为20海里/小时,先沿正东方向航行3小时后,到达C港口接旅客,停留1小时后再转向北偏东30°方向开往B岛,其速度仍为20海里/小时.
(1)求海岛B到航线AC的距离;
(2)甲船在航行至P处,发现乙船在其正东方向的Q处,问此时两船相距多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠ACB=90°,BC=2,AC=4,点D在射线BC上,以点D为圆心,BD为半径画弧交边AB于点E,过点E作EF⊥AB交边AC于点F,射线ED交射线AC于点G.
(1)求证:△EFG∽△AEG;
(2)设FG=x,△EFG的面积为y,求y关于x的函数解析式并写出定义域;
(3)联结DF,当△EFD是等腰三角形时,请直接写出FG的长度.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(1)求该二次函数图象与x轴的交点坐标;
(2)若m<0,当1≤x≤4时,y的最大值是2,求当1≤x≤4时,y的最小值;
(3)已知P(2,![]() ),Q(4,
),Q(4,![]() )为平面直角坐标系中两点,当抛物线与线段PQ有公共点时,请求出m的取值范围.
)为平面直角坐标系中两点,当抛物线与线段PQ有公共点时,请求出m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com