
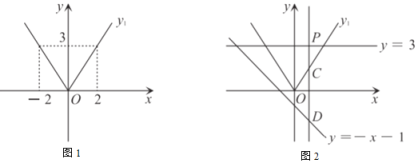
【题目】(1)写出图1中函数图象的解析式![]() ;
;

(2)如图2,过直线![]() 上一点
上一点![]() 作
作![]() 轴的垂线交
轴的垂线交![]() 的图象于点
的图象于点![]() ,交直线
,交直线![]() 于点
于点![]() .
.
①试比较![]() 与
与![]() 的大小,并证明你的结论;
的大小,并证明你的结论;
②若![]() 时,求
时,求![]() 的值.
的值.
【答案】(1)![]() 或
或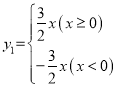 ;(2)①当
;(2)①当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,证明见解析;②
,证明见解析;②![]() 或
或![]() .
.
【解析】
(1)应用待定系数法,分类讨论求解析式;
(2)①观察点P的位置,可以发现随着点P的运动,点C的坐标表示发生变化,因而进行分类讨论求m范围即可;
②由图象可知,点C在点D上方,分别根据m>0和m≤0时的CD值分类讨论求m范围.
解:(1)如图:
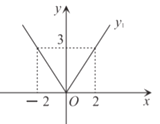
设![]() ,则
,则
当![]() 时,图像经过点(2,3),
时,图像经过点(2,3),
∴![]() ,解得:
,解得:![]() ,
,
∴![]() ;
;
当![]() 时,图像经过点(-2,3),
时,图像经过点(-2,3),
∴![]() ,解得:
,解得:![]() ,
,
∴![]() ;
;
∴函数的解析式为:![]() 或
或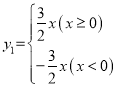 ;
;
故答案为:![]() 或
或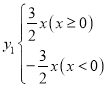 ;
;
![]() 由已知得,点C坐标为(m,
由已知得,点C坐标为(m,![]() m),点D坐标为(m,-m-1),则PD=3-(-m-1)=4+m,
m),点D坐标为(m,-m-1),则PD=3-(-m-1)=4+m,
当点C在直线y=3下方时或在直线y=3上时,由图象可知PC<PD,
当点C在直线y=3上方时,CP=![]() m-3,
m-3,
∴当CP=PD时,![]() m-3=4+m,
m-3=4+m,
解得:m=14,
当CP>PD时,![]() m-3>4+m,
m-3>4+m,
解得:m>14,
当CP<PD时,![]() m-3<4+m,
m-3<4+m,
解得:m<14
综上所述,当0<m<14时,CP<PD,当m=14时,CP=PD,当m>14时,CP>PD;
②当m>0时,点C坐标为(m,![]() m),点D坐标为(m,-m-1),
m),点D坐标为(m,-m-1),
∴![]() ,
,
![]() ,
,
![]() ;
;
当m≤0时,点C坐标为(m,![]() m),点D坐标为(m,-m-1),
m),点D坐标为(m,-m-1),
则CD=![]() m-(-m-1)=
m-(-m-1)=![]() m+1=3,
m+1=3,
解得:m=![]() ;
;
∴当![]() 时,
时,![]() 的值为
的值为![]() 或
或![]() ;
;


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,图1为一个长方体,AB=AD=16,AE=6,图2为左图的表面展开图,请根据要求回答问题:
(1)面“学”的对面是面什么?
(2)图1中,M、N为所在棱的中点,试在图2中画出点M、N的位置; 并求出图2中△ABN的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() 有实数根.
有实数根.
(1)求m的值;
(2)先作![]() 的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式;
的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式;
(3)在(2)的条件下,当直线y=2x+n(n≥m)与变化后的图象有公共点时,求![]() 的最大值和最小值.
的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在七年级设立了六个课外兴趣小组,每个参加者只能参加一个兴趣小组,下面是六个兴趣小组不完整的频数分布直方图和扇形统计图.根据图中信息,解决下列问题:

(1)七年级共有 人参加了兴趣小组;
(2)体育兴趣小组对应扇形圆心角的度数为 ;
(3)以各小组人数组成一组新数据,求这组新数据的中位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
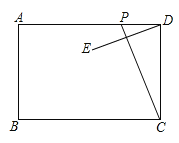
【题目】如图,已知矩形ABCD中,AB=6,AD=10,动点P从点D出发,在边DA上以每秒1个单位的速度向点A运动,连接CP,作点D关于直线PC的对称点E,设点P的运动时间为t(x),当P,E,B三点在同一直线上时对应t的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
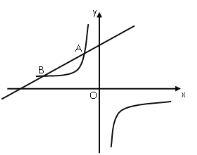
【题目】如图,一次函数![]() (
(![]() 为常数,且
为常数,且![]() )的图像与反比例函数
)的图像与反比例函数![]() 的图像交于
的图像交于![]() ,
,![]() 两点.
两点.
(1)求一次函数的表达式;
(2)若将直线![]() 向下平移
向下平移![]() 个单位长度后与反比例函数的图像有且只有一个公共点,求
个单位长度后与反比例函数的图像有且只有一个公共点,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
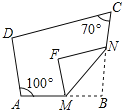
【题目】如图,四边形ABCD中,∠BAD=100°,∠BCD=70°,点M,N分别在AB,BC上,将△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业为了提高工人劳动的积极性,决定对工人的月工资进行调整.已知该企业有 n 名工人,调整后的月工资 y(元)与调整前的月工资 x(元)满足一次函数关系,如下表:

(1)求 y 与 x 的函数关系式;
(2)若某名工人调整前月工资是4800元,那么调整后这名工人月工资增加了多少元?
(3)这 ![]() 名工人调整前、后的平均月工资分别为
名工人调整前、后的平均月工资分别为![]() ,
,![]() ,猜想
,猜想![]() 与
与![]() 的关系式,并写出推导过程.
的关系式,并写出推导过程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com