练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

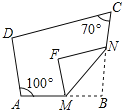
    【题目】如图，四边形ABCD中，∠BAD=100°，∠BCD=70°，点M，N分别在AB，BC上，将△BMN沿MN翻折，得△FMN，若MF∥AD，FN∥DC，求∠B的度数．

    【答案】95°

    【解析】

    根据两直线平行，同位角相等求出∠BMF、∠BNF，再根据翻折的性质求出∠BMN和∠BNM，然后利用三角形的内角和定理列式计算即可得解．

    解：∵MF∥AD，FN∥DC，

    ∴∠BMF=∠A=100°，∠BNF=∠C=70°，

    ∵△BMN沿MN翻折得△FMN，

    ∴∠BMN=∠BMF=×100°=50°，

    ∠BNM=∠BNF=×70°=35°，

    在△BMN中，∠B=180°﹣（∠BMN+∠BNM）=180°﹣（50°+35°）=180°﹣85°=95°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，有一个水池，其底面是边长为16尺的正方形，一根芦苇AB生长在它的正中央，高出水面部分BC的长为2尺，如果把该芦苇沿与水池边垂直的方向拉向岸边，那么芦苇的顶部B恰好碰到岸边的B′，则这根芦苇AB的长是（　　）

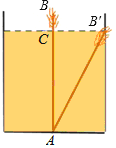
    A. 15尺B. 16尺C. 17尺D. 18尺

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）写出图1中函数图象的解析式 ；

    （2）如图2，过直线上一点作轴的垂线交的图象于点，交直线于点．

    ①试比较与的大小，并证明你的结论；

    ②若时，求的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】不能构成三角形的三条整数长度的线段的长度和的最小值为1+1+2=4；若四条整数长度的线段中，任意三条不能构成三角形，则该四条线段的长度和的最小值为1+1+2+3=7；……，依此规律，若八条整数长度的线段中，任意三条不能构成三角形，则该八条线段的长度和的最小值为________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，A1，A2，A3，…，An为AC边上不同的n个点，首先连接BA1，图中出现了3个不同的三角形，再连接BA2，图中便有6个不同的三角形，……

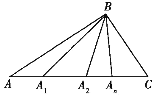
    （1）完成下表：

    连接个数

    1

    2

    3

    4

    5

    6

    出现三角形个数

    3

    6

    （2）若出现了45个三角形，则共连接了_____个点?若一直连接到An，则图中共有______个三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

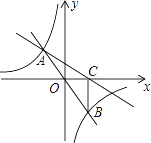
    【题目】如图，直线y=mx（m为常数，且m≠0）与双曲线y= （k为常数，且k≠0）相交于A（﹣2，6），B两点，过点B作BC⊥x轴于点C，连接AC，则△ABC的面积为________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

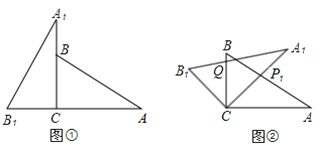
    【题目】将两块全等的三角板如图①摆放，其中∠A1CB1=∠ACB=90°，∠A1=∠A=30°．

    （1）将图①中的△A1B1C顺时针旋转45°得图②，点P1是A1C与AB的交点，点Q是A1B1与BC的交点，求证：CP1=CQ；

    （2）在图②中，若AP1=2，则CQ等于多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠ACB＝90°，∠ABC＝30°，△CDE是等边三角形，点D在边AB上．

    （1）如图1，当点E在边BC上时，求证DE＝EB；

    （2）如图2，当点E在△ABC内部时，猜想ED和EB数量关系，并加以证明；

    （3）如图3，当点E在△ABC外部时，EH⊥AB于点H，过点E作GE∥AB，交线段AC的延长线于点G，AG＝5CG，BH＝3．求CG的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知在△ABC中，∠ACB=90°，BC=2，AC=4，点D在射线BC上，以点D为圆心，BD为半径画弧交边AB于点E，过点E作EF⊥AB交边AC于点F，射线ED交射线AC于点G．

    （1）求证：△EFG∽△AEG；

    （2）设FG=x，△EFG的面积为y，求y关于x的函数解析式并写出定义域；

    （3）联结DF，当△EFD是等腰三角形时，请直接写出FG的长度．

    查看答案和解析>>

    同步练习册答案