
【题目】抛物线y=a(x+2)2+c与x轴交于A,B两点,与y轴负半轴交于点C,已知点A(-1,0),OB=OC.
(1)求此抛物线的解析式;
(2)若把抛物线与直线y=-x-4的交点称为抛物线的不动点,若将此抛物线平移,使其顶点为(m,2m),当m满足什么条件时,平移后的抛物线总有不动点;
(3)Q为直线y=-x-4上一点,在此抛物线的对称轴上是否存在一点P,使得∠APB=2∠AQB,且这样的Q点有且只有一个?若存在,请求出点P的坐标;若不存在,请说明理由.
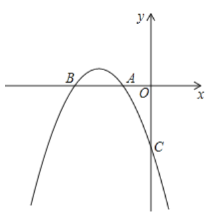
【答案】(1) y=x![]() 4x3;(2) m≥
4x3;(2) m≥![]() ;(3) P(2,2+
;(3) P(2,2+![]() )或(2,2
)或(2,2![]() ).
).
【解析】
(1)根据函数的解析式可以得到函数的对称轴是x=-2,则B点的坐标可以求得,求得OB的长,则C的坐标可以求得,把A、C的坐标代入函数解析式即可求得;
(2)根据平移后抛物线的顶点坐标设出抛物线的顶点式,然后根据抛物线与直线的有交点,列方程组,最后根据△≥0,求出m的取值范围;
(3)设P(-2,m),以P为圆心的圆与直线y=-x-4相切,根据切线的性质即可求解.
(1)由抛物线y=a(x+2)![]() +c可知,其对称轴为x=2,
+c可知,其对称轴为x=2,
∵点A坐标为(1,0),
∴点B坐标为(3,0),
∵OB=OC,
∴C点坐标为(0,3).
将A(1,0)、C(0,3)分别代入解析式得,
a+c=0
4a+c=3,
解得a=1,c=1
则函数解析式为y=x![]() 4x3.
4x3.
(2)由题意平移后的抛物线的解析式为y=(xm)![]() +2m,
+2m,
由x4=(xm)![]() +2m,得到:x
+2m,得到:x![]() (2m+1)x+m
(2m+1)x+m![]() 2m4=0,
2m4=0,
∵平移后的抛物线总有不动点,
∴△≥0,
∴4m![]() +4m+14(m
+4m+14(m![]() 2m4)0,
2m4)0,
解得m≥![]() .
.
(3)如图,设P(2,m),以P为圆心的圆与直线y=x4相切,切点为D,直线y=x4交抛物线的对称轴于E,则E(2,2)
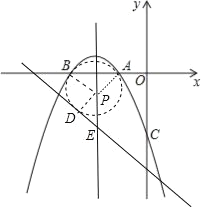
∴PE=m+2,PD=![]() PE,
PE,
∵PA=PD,
∴![]() =1+m
=1+m![]() ,
,
解得m=2±![]() ,故P(2,2+
,故P(2,2+![]() )或(2,2
)或(2,2![]() ).
).


 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案科目:初中数学 来源: 题型:
【题目】5G网络是第五代移动通信网络,它将推动我国数字经济发展迈上新台阶. 据预测,2020年到2030年中国5G直接经济产出和间接经济产出的情况如下图所示.
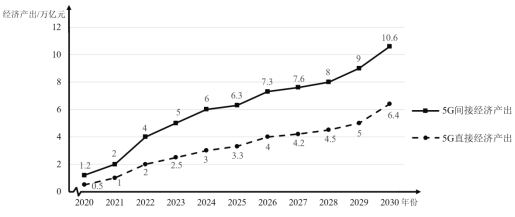
根据上图提供的信息,下列推断不合理的是( )
A.2030年5G间接经济产出比5G直接经济产出多4.2万亿元
B.2020年到2030年,5G直接经济产出和5G间接经济产出都是逐年增长
C.2030年5G直接经济产出约为2020年5G直接经济产出的13倍
D.2022年到2023年与2023年到2024年5G间接经济产出的增长率相同
查看答案和解析>>
科目:初中数学 来源: 题型:
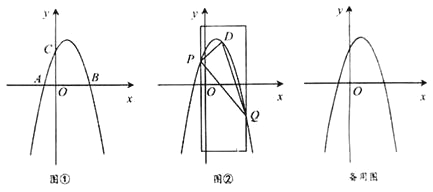
【题目】如图①,在平面直角坐标系xOy 中,抛物线y=ax2+bx+3经过点A(-1,0) 、B(3,0) 两点,且与y轴交于点C
.
(1)求抛物线的表达式;
(2)如图②,用宽为4个单位长度的直尺垂直于x轴,并沿x轴左右平移,直尺的左右两边所在的直线与抛物线相交于P、 Q两点(点P在点Q的左侧),连接PQ,在线段PQ上方抛物线上有一动点D,连接DP、DQ.
①若点P的横坐标为![]() ,求△DPQ面积的最大值,并求此时点D 的坐标;
,求△DPQ面积的最大值,并求此时点D 的坐标;
②直尺在平移过程中,△DPQ面积是否有最大值?若有,求出面积的最大值;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了丰富学生的校园文化生活,学校开设了书法、体育、美术音乐共四门选修课程.为了合理的分配教室,教务处问卷调查了部分学生,并将了解的情况绘制成如下不完整的统计图:
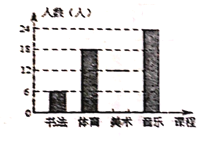
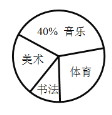
(1)参与问卷调查的共有________人,其中选修美术的有________人,选修体育的学生人数对应扇形统计图中圆心角的度数为________.
(2)补全条形统计图;
(3)若每人必须选修一门课程,且只能选一门,已知小红没有选体育,小刚没有选修书法和美术,则他们选修同一门课程的概率是多少,列树状图或列表法求解.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2013年四川绵阳12分)如图,已知矩形OABC中,OA=2,AB=4,双曲线![]() (k>0)与矩形两边AB、BC分别交于E、F.
(k>0)与矩形两边AB、BC分别交于E、F.

(1)若E是AB的中点,求F点的坐标;
(2)若将△BEF沿直线EF对折,B点落在x轴上的D点,作EG⊥OC,垂足为G,证明△EGD∽△DCF,并求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节是我国的传统节日,益民食品厂为了解市民对去年销量较好的花生粽子、水果粽子、豆沙粽子、红枣粽子(分别用A、B、C、D表示)这四种不同口味的粽子的喜爱情况,对某居民区的市民进行了抽样调查,并根据调查结果绘制了如下两幅不完整的统计图.
(1)本次参加抽样调查的居民有多少人?
(2)将两幅统计图补充完整;
(3)小明喜欢吃花生粽子和红枣粽子,妈妈为他准备了四种粽子各一个,请用“列表法”或“画树形图”的方法,求出小明同时选中花生粽子和红枣粽子的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小明要测量河内小岛B到河边公路AD的距离,在点A处测得∠BAD=37°,沿AD方向前进150米到达点C,测得∠BCD=45°. 求小岛B到河边公路AD的距离.
(参考数据:sin37°≈ 0.60,cos37° ≈ 0.80,tan37° ≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系xOy中,点A的坐标为(﹣2,2),点B的坐标为(6,6),抛物线经过A、O、B三点,连结OA、OB、AB,线段AB交y轴于点E.
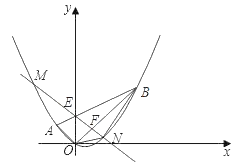
(1)求点E的坐标;
(2)求抛物线的函数解析式;
(3)点F为线段OB上的一个动点(不与点O、B重合),直线EF与抛物线交于M、N两点(点N在y轴右侧),连结ON、BN,当点F在线段OB上运动时,求△BON面积的最大值,并求出此时点N的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com