
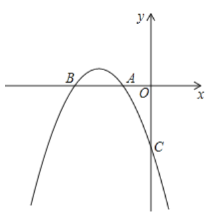
ЁОЬтФПЁПШчЭМЃЌЦНУцжБНЧзјБъЯЕxOyжаЃЌЕуAЕФзјБъЮЊЃЈЉ2ЃЌ2ЃЉЃЌЕуBЕФзјБъЮЊЃЈ6ЃЌ6ЃЉЃЌХзЮяЯпОЙ§AЁЂOЁЂBШ§ЕуЃЌСЌНсOAЁЂOBЁЂABЃЌЯпЖЮABНЛyжсгкЕуEЃЎ
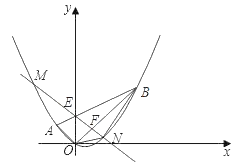
ЃЈ1ЃЉЧѓЕуEЕФзјБъЃЛ
ЃЈ2ЃЉЧѓХзЮяЯпЕФКЏЪ§НтЮіЪНЃЛ
ЃЈ3ЃЉЕуFЮЊЯпЖЮOBЩЯЕФвЛИіЖЏЕуЃЈВЛгыЕуOЁЂBжиКЯЃЉЃЌжБЯпEFгыХзЮяЯпНЛгкMЁЂNСНЕуЃЈЕуNдкyжсгвВрЃЉЃЌСЌНсONЁЂBNЃЌЕБЕуFдкЯпЖЮOBЩЯдЫЖЏЪБЃЌЧѓЁїBONУцЛ§ЕФзюДѓжЕЃЌВЂЧѓГіДЫЪБЕуNЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉEЃЈ0ЃЌ3ЃЉЃЈ2ЃЉyЃН![]() x2Љ
x2Љ![]() xЃЈ3ЃЉ
xЃЈ3ЃЉ![]()
ЁОНтЮіЁП
ЃЈ1ЃЉЯШЧѓГіжБЯпABЕФНтЮіЪНЃЌДгЖјИљОнЕуEЕФКсзјБъЮЊ0ЃЌПЩЕУЦфзнзјБъЃЛ
ЃЈ2ЃЉИљОнХзЮяЯпЙ§дЕуЃЌПЩЩшХзЮяЯпЮЊyЃНmx2+nxЃЌДњШыAЁЂBЕФзјБъЃЌМДПЩШЗЖЈХзЮяЯпНтЮіЪНЃЛ
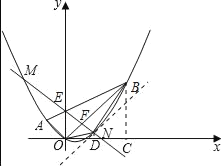
ЃЈ3ЃЉжЛашШЗЖЈБпOBЩЯИпЕФзюДѓжЕМДПЩЃЌЩшЙ§ЕуNЧвгыжБЯпOBЦНааЕФжБЯпНтЮіЪНЮЊyЃНx+cЃЌЕБЧвНіЕБжБЯпyЃНx+cгыХзЮяЯпyЃН![]() ЯрЧаЪБЁїBONЕФУцЛ§зюДѓЃЌШЗЖЈШЁЕУзюДѓЪБЕуNЕФзјБъЃЌдйгЩSЁїBONЃНSЁїOCBЉSЁїODNЉSЬнаЮNDCBЃЌМДПЩЕУГіД№АИЃЎ
ЯрЧаЪБЁїBONЕФУцЛ§зюДѓЃЌШЗЖЈШЁЕУзюДѓЪБЕуNЕФзјБъЃЌдйгЩSЁїBONЃНSЁїOCBЉSЁїODNЉSЬнаЮNDCBЃЌМДПЩЕУГіД№АИЃЎ
ЃЈ1ЃЉЩшЕуAЁЂBЫљдкЕФжБЯпНтЮіЪНЮЊyЃНkx+bЃЌ
дђ![]()
НтЕУЃК ![]()
МДжБЯпABЕФНтЮіЪНЮЊyЃН![]() x+3ЃЌ
x+3ЃЌ
СюxЃН0ЃЌЕУyЃН3ЃЌ
ЙЪEЃЈ0ЃЌ3ЃЉЃЎ
ЃЈ2ЃЉЁпЫљЧѓХзЮяЯпЙ§дЕуЃЌ
ЁрЩшЫљЧѓХзЮяЯпЮЊyЃНmx2+nxЃЌ
НЋЕуAЁЂBЕФзјБъДњШыЃЌЕУЃК![]()
НтЕУЃК 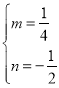
ЁрХзЮяЯпЕФНтЮіЪНЮЊ![]()
ЃЈ3ЃЉВЛФбЧѓГіжБЯпOBЕФНтЮіЪНЮЊyЃНxЃЌ
вЊЪЙЁїBONЕФУцЛ§зюДѓЃЌжЛашOBБпЩЯЕФИпзюДѓМДПЩЃЌ
ЩшЙ§ЕуNЧвгыжБЯпOBЦНааЕФжБЯпНтЮіЪНЮЊyЃНx+cЃЌ
ЕБЧвНіЕБжБЯпyЃНx+cгыХзЮяЯп![]() ЯрЧаЪБЁїBONЕФУцЛ§зюДѓЃЌ
ЯрЧаЪБЁїBONЕФУцЛ§зюДѓЃЌ
гЩ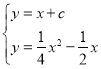 ЃЌЯћШЅyВЂећРэЕУx2Љ6xЉ4cЃН0ЃЌ
ЃЌЯћШЅyВЂећРэЕУx2Љ6xЉ4cЃН0ЃЌ
ЕБЁїЃЈЉ6ЃЉ2Љ4ЁС1ЁСЃЈЉ4cЃЉЃН0ЪБЃЌЗНГЬx2Љ6xЉ4cЃН0ЕФНтЮЊxЃН3ЃЌ
НЋxЃН3ДњШы![]() ЃЌЕУyЃН
ЃЌЕУyЃН![]() ЃЌ
ЃЌ
ЁрNЃЈ3ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
Й§ЕуBЁЂNЗжБ№зїBCЁЭxжсгкЕуCЃЌNDЁЭxжсгкЕуDЃЌ
SЁїBONЃНSЁїOCBЉSЁїODNЉSЬнаЮNDCBЃН![]()



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПХзЮяЯпy=aЃЈx+2ЃЉ2+cгыxжсНЛгкAЃЌBСНЕуЃЌгыyжсИКАыжсНЛгкЕуCЃЌвбжЊЕуAЃЈ-1ЃЌ0ЃЉЃЌOB=OCЃЎ
ЃЈ1ЃЉЧѓДЫХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉШєАбХзЮяЯпгыжБЯпy=-x-4ЕФНЛЕуГЦЮЊХзЮяЯпЕФВЛЖЏЕуЃЌШєНЋДЫХзЮяЯпЦНвЦЃЌЪЙЦфЖЅЕуЮЊЃЈmЃЌ2mЃЉЃЌЕБmТњзуЪВУДЬѕМўЪБЃЌЦНвЦКѓЕФХзЮяЯпзмгаВЛЖЏЕуЃЛ
ЃЈ3ЃЉQЮЊжБЯпy=-x-4ЩЯвЛЕуЃЌдкДЫХзЮяЯпЕФЖдГЦжсЩЯЪЧЗёДцдквЛЕуPЃЌЪЙЕУЁЯAPB=2ЁЯAQBЃЌЧветбљЕФQЕугаЧвжЛгавЛИіЃПШєДцдкЃЌЧыЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдке§ЗНаЮABCDжаЃЌЕуEЃЌFНЋЖдНЧЯпACШ§ЕШЗжЃЌЧвAC=12ЃЌЕуPдке§ЗНаЮЕФБпЩЯЃЌдђТњзуPE+PF=9ЕФЕуPЕФИіЪ§ЪЧЃЈ ЃЉ
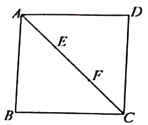
A. 0B. 4C. 6D. 8
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
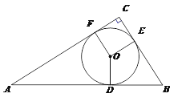
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCжаЃЌЁЯCЃН90ЁуЃЌЁбOЪЧRtЁїABCЕФФкЧадВЃЌЧаЕуЮЊDЁЂEЁЂF.
ЃЈ1ЃЉЧѓжЄЃКЫФБпаЮOECFЪЧе§ЗНаЮЃЛ
ЃЈ2ЃЉШєAFЃН10ЃЌBEЃН3ЃЌЧѓЁбOЕФУцЛ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
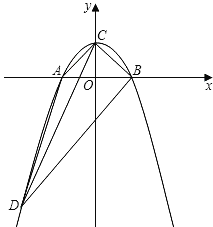
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃНax2+bx+1гыxжсНЛгкСНЕуAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ1ЃЌ0ЃЉЃЌгыyжсНЛгкЕуCЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЙ§ЕуBзїBDЁЮCAХзЮяЯпНЛгкЕуDЃЌЧѓЫФБпаЮACBDЕФУцЛ§ЃЛ
ЃЈ3ЃЉдкxжсЯТЗНЕФХзЮяЯпЩЯЪЧЗёДцдкЕуMЃЌЙ§MзїMNЁЭxжсгкЕуNЃЌЪЙвдAЁЂMЁЂNЮЊЖЅЕуЕФШ§НЧаЮгыЁїBCDЯрЫЦЃПШєДцдкЃЌдђЧѓГіЕуMЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЭМЂйЁЂЭМЂкЁЂЭМЂлЖМЪЧ4ЁС4ЕФе§ЗНаЮЭјИёЃЌУПИіаЁе§ЗНаЮЕФБпГЄОљЮЊ1ЃЌУПИіаЁе§ЗНаЮЕФЖЅЕуНазіИёЕуЃЌЯпЖЮABЕФЖЅЕуЖМдкИёЕуЩЯ.
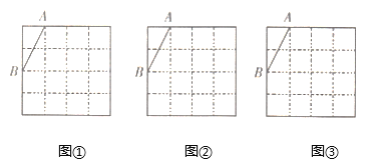
ЃЈ1ЃЉРћгУЭМЂйвдABЮЊБпЛвЛИіУцЛ§зюДѓЕФЦНааЫФБпаЮЃЌЧветИіЦНааЫФБпаЮЕФЦфЫћСНИіЖЅЕудкИёЕуЩЯЃЛ
ЃЈ2ЃЉРћгУЭМЂквдABЮЊБпЛвЛИіУцЛ§ЮЊ4ЕФЦНааЫФБпаЮЃЌЧветИіЦНааЫФБпаЮЕФЦфЫћСНИіЖЅЕудкИёЕуЩЯЃЛ
ЃЈ3ЃЉРћгУЭМЂлвдABЮЊБпЛвЛИіУцЛ§ЮЊ4ЕФСтаЮЃЌЧветИіСтаЮЕФЦфЫћСНИіЖЅЕудкИёЕуЩЯЁЃ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЈвхЃКдкЦНУцжБНЧзјБъЯЕжаЃЌЭМаЮGЩЯЕуPЃЈxЃЌyЃЉЕФзнзјБъyгыЦфКсзјБъxЕФВюy-xГЦЮЊЕуPЕФЁАзјБъВюЁБЃЌЖјЭМаЮGЩЯЫљгаЕуЕФЁАзјБъВюЁБжаЕФзюДѓжЕГЦЮЊЭМаЮGЕФЁАЬиеїжЕЁБ
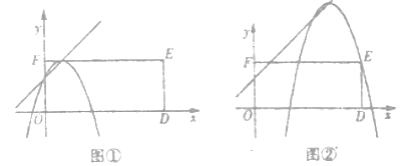
ЃЈ1ЃЉЕуAЃЈ2ЃЌ6ЃЉЕФЁАзјБъВюЁБЮЊ________ЃЛ
ЃЈ2ЃЉЧѓХзЮяЯпy=-x2+5.x+4ЕФЁАЬиеїжЕЁБЃЛ
ЃЈ3ЃЉФГЖўДЮКЏЪ§y=-x2+bx+cЃЈcЁй0ЃЉЕФЁАЬиеїжЕЁБЮЊ-1ЃЌЕуBгыЕуCЗжБ№ЪЧДЫЖўДЮКЏЪ§ЕФЭМЯѓгыxжсКЭyжсЕФНЛЕуЃЌЧвЕуBгыЕуCЕФЁАзјБъВюЁБЯрЕШЃЌЧѓДЫЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ4ЃЉЖўДЮКЏЪ§y=-x2+px+qЕФЭМЯѓЕФЖЅЕудкЁАзјБъВюЁБЮЊ2ЕФвЛДЮКЏЪ§ЕФЭМЯѓЩЯЃЌЫФБпаЮDEFOЪЧОиаЮЃЌЕуEЕФзјБъЮЊЃЈ7ЃЌ3ЃЉЃЌЕуOЮЊзјБъдЕуЃЌЕуDдкxжсЩЯЕуЯТдкxжсЩЯЃЌЕБЖўДЮКЏЪ§y=-x2+px+qЕФЭМЯѓгыОиаЮЕФБпжЛгаШ§ИіНЛЕуЪБЃЌЧѓДЫЖўДЮКЏЪ§ЕФНтЮіЪНМАЬиеїжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
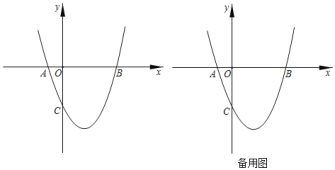
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃНax2+bx+cгыxжсНЛгкAЃЈЉ1ЃЌ0ЃЉBЃЈ3ЃЌ0ЃЉСНЕуЃЌгыyжсНЛгкЕуCЃЈ0ЃЌЉ3ЃЉ
ЃЈ1ЃЉЧѓГіИУХзЮяЯпЕФКЏЪ§ЙиЯЕЪНМАЖдГЦжс
ЃЈ2ЃЉЕуPЪЧХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЩшЕуPЕФКсзјБъЮЊt ЃЈ0ЃМtЃМ3ЃЉЃЎЕБЁїPCBЕФУцЛ§ЕФзюДѓжЕЪБЃЌЧѓЕуPЕФзјБъ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
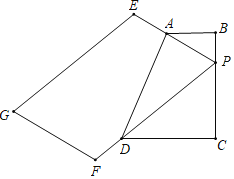
ЁОЬтФПЁПдкЫФБпаЮABCDжаЃЌABЁЮCDЃЌBCЁЭCDЃЌABЃН2ЃЌCDЃН3ЃЌдкBCЩЯШЁЕуPЃЈPгыBЁЂCВЛжиКЯЃЉСЌНгPAбгГЄжСEЃЌЪЙPAЃН2AEЃЌСЌНгPDВЂбгГЄжСFЃЌЪЙPDЃН3FDЃЌвдPEЁЂPFЮЊБпзїЦНааЫФБпаЮЃЌСэвЛИіЖЅЕуЮЊGЃЌдђPGГЄЖШЕФзюаЁжЕЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com