
����Ŀ�����壺��ƽ��ֱ������ϵ�У�ͼ��G�ϵ�P��x��y����������y���������x�IJ�y-x��Ϊ��P���������������ͼ��G�����е������������е����ֵ��Ϊͼ��G��������ֵ��
��1����A��2��6�������������Ϊ________��
��2����������y=-x2+5.x+4��������ֵ����
��3��ij���κ���y=-x2+bx+c��c��0����������ֵ��Ϊ-1����B���C�ֱ��Ǵ˶��κ�����ͼ����x���y��Ľ��㣬�ҵ�B���C�������������ȣ���˶��κ����Ľ���ʽ��
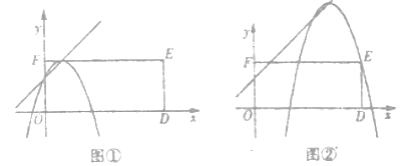
��4�����κ���y=-x2+px+q��ͼ��Ķ��������������Ϊ2��һ�κ�����ͼ���ϣ��ı���DEFO�Ǿ��Σ���E������Ϊ��7��3������OΪ����ԭ�㣬��D��x���ϵ�����x���ϣ������κ���y=-x2+px+q��ͼ������εı�ֻ����������ʱ����˶��κ����Ľ���ʽ������ֵ.
���𰸡���1��4����2��8����3��y=-x2+3x-2����4��y=-��x-5��2+7��![]()
��������
��1��������Ŀ�еĹ涨�ý��ۣ�
��2�����ݶ������y-x�ǹ���x�Ķ��κ�����Ȼ�����ö��κ���������������ۣ�
��3���������������y��Ľ���C��0��c�������B������Ϊ��-c��0��,�ѵ�B�����������κ�������ʽ�õ�b=1-c���ٽ�b=1-c������κ�������ʽ���������ֵy-x�Ĵ���ʽ��Ȼ��������ֵΪ-1���c��ֵ���̶����b��ֵ������������κ�������ʽ��
��4����������������Ϊ2��һ�κ����Ľ���ʽΪy=x+2���ɶ��κ���y=-x2+px+q��ͼ��Ķ�����ֱ��y=x+2�ϣ��ö���ʽ������κ���Ϊy=-��x-m��2+m+2.����������¶��κ�����ͼ�������ֻ���������㣺�������߶�����ֱ��y=x+2��FE�Ľ�����ʱ����ͼ�٣������������Ҳಿ�־�����Eʱ����ͼ�ڣ�.Ȼ��ֱ�ѣ�1��3������7��3���ֱ����y=-��x-m��2+m+2�����m��ֵ������������κ�������ʽ���̶����������ֵ.
��1����������������Ķ���ã�6-2=4��
��2��y-x=-x2+5x+4-x=-x2+4x+4=-��x-2��2+8������ֵ��8
��3�������⣬�õ�C������Ϊ��0��c����
�ߵ�B���C�������������ȣ�
��B��-c.0������B��-c��0������y=-x2+bx+c����0=-��-c��2+b����-c��+c��
��b=1-c��
��y=-x2+��1-c��x+c��
�߶��κ���y=-x2+��1-c��x+c��������ֵ��Ϊ-1.
��y-x=-x2+(1-c)x+c-x=-x2-cx+c��
��![]() =-1��
=-1��
��c=-2��
��b=3��
����κ����Ľ���ʽΪy=-x2+3x-2
��4���⣺���������Ϊ2��һ�κ���Ϊy=x+2��
�߶��κ���y=-x2+px+q��ͼ��Ķ�����ֱ��y=x+2�ϣ�
������κ���Ϊy=-��x-m��2+m+2��
���κ�����ͼ����������������㣬��ͼ�١��ڣ��ѣ�1��3������y=-��x-m��2+m+2����3=-��1-x��2+m+2�����m1=1��m2=2����ȥ����
����κ����Ľ���ʽΪy=-��x-1��2+3��
��y-x=-��x-1��2+3-x=-x2+x+2=-��x-![]() ��2+
��2+![]() ������ֵ��
������ֵ��![]() ��
��
�ѣ�7��3������y=-��x-m��2+m+2����3=-��7-m��2+m+2�����m1=5��m2=10����ȥ����
���κ����Ľ�����Ϊy=-��x-5��2+7��
��y-x=-(x-5)2+7-x=-x2+9x-18=-��x-![]() ��2+
��2+![]() ������ֵ��
������ֵ��![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ����
����![]() �͵�
�͵�![]() ���Ҷ����ڵ������ޣ���
���Ҷ����ڵ������ޣ���![]() ����
����![]() ��ȡֵ��Χ�ǣ� ��
��ȡֵ��Χ�ǣ� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
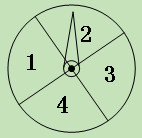
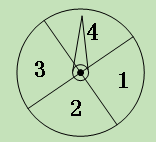
����Ŀ����11��Т�У�ѧ������ѧ������һ��ת����Ϸ.��ͼ��������ȫ��ͬ��ת�̣�ÿ��ת�̱��ֳ������ȵ��ĸ����ֱ���������1������2������3������4����ʾ.�̶�ָ�룬ͬʱת������ת�̣���������ֹͣ������ָ����ָ���ֵĻ�Ϊ���������ʤ������ָ����ָ���ֵĻ�Ϊż�������һ�ʤ����ָ��ָ�����εķֽ��ߣ�����תһ��.�ڸ���Ϸ���һ�ʤ�ĸ����� �� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ��ֱ������ϵxOy�У���A������Ϊ����2��2������B������Ϊ��6��6���������߾���A��O��B���㣬����OA��OB��AB���߶�AB��y���ڵ�E��
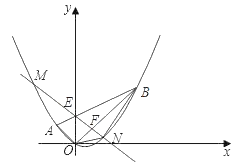
��1�����E�����ꣻ
��2���������ߵĺ�������ʽ��
��3����FΪ�߶�OB�ϵ�һ�����㣨�����O��B�غϣ���ֱ��EF�������߽���M��N���㣨��N��y���Ҳࣩ������ON��BN������F���߶�OB���˶�ʱ�����BON��������ֵ���������ʱ��N�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ����뷴����������ͼ���ڵ�A��-4��-2����B��a��4����ֱ��AB��y���ڵ�C������QA��OB.
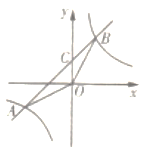
��1�����������Ľ���ʽ�͵�B�����꣺
��2������ͼ��ش𣬵�x��ȡֵ��ʲô��Χ��ʱ��һ�κ�����ֵ���ڷ�����������ֵ��
��3������AOB�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����֪![]() �ǵ���ֱ�������Σ�
�ǵ���ֱ�������Σ�![]() ����D��BC���е�
����D��BC���е�![]() ��������DEFG��ʹ��A��C�ֱ���DG��DE�ϣ�����AE��BG��
��������DEFG��ʹ��A��C�ֱ���DG��DE�ϣ�����AE��BG��
![]() �Բ����߶�BG��AE��������ϵ��______��
�Բ����߶�BG��AE��������ϵ��______��
![]() ��������DEFG�Ƶ�D��ʱ�뷽����ת
��������DEFG�Ƶ�D��ʱ�뷽����ת![]() ��
��
![]() �ж�
�ж�![]() �еĽ����Ƿ���Ȼ������������ͼ2֤����Ľ��ۣ�
�еĽ����Ƿ���Ȼ������������ͼ2֤����Ľ��ۣ�
![]() ��
��![]() ����AEȡ���ֵʱ����AF��ֵ��
����AEȡ���ֵʱ����AF��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ��ʾ��ƽ��ֱ������ϵ�У���֪��A����3����3������B����1����3������C����1����1��
��1��������ABC��
��2���Ե�CΪ��ת���ģ���������ABC˳ʱ����ת90�ȵġ�A1B1C��������߶�CAɨ���������
��3����OΪλ�����ģ��ڵ�һ������������A2B2C2ʹ��A2B2C2���ABCλ�ƣ���λ�Ʊ�Ϊ2����д��A2������꣮
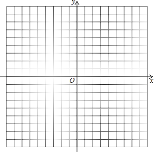
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Ȥζ�˶���������Ͷ������Ŀ�У���У���꼶�˸����Ͷ���ɼ�![]() ��λ����
��λ����![]() �ֱ�Ϊ��24��20��19��20��22��23��20��
�ֱ�Ϊ��24��20��19��20��22��23��20��![]() �����������е���������λ���ֱ���
�����������е���������λ���ֱ���![]() ����
����![]()
A. 22����20�� B. 22����21�� C. 20����21�� D. 20����22��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���һ�����ڵĵ�P��ֱ��y��![]() x�ϣ�����P��ֱ�߽�x���������ڵ�A����ֱ��y��3x�ڵ�B����B�ڵ�һ�����ڣ�
x�ϣ�����P��ֱ�߽�x���������ڵ�A����ֱ��y��3x�ڵ�B����B�ڵ�һ�����ڣ�
(1)��ͼ1������OAB��90��ʱ����![]() ��ֵ��
��ֵ��
(2)����A������Ϊ(6��0)����BP��2APʱ��������A��������y����x2+mx���·�ƽ�ƣ�ʹ������B����ƽ�Ƶķ���;��룮
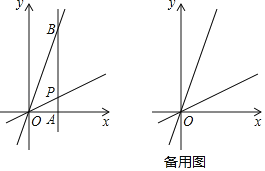
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com