
【题目】如图,已知钝角![]() .
.
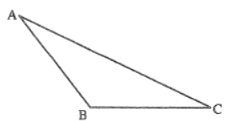
(1)过钝角顶点![]() 作
作![]() ,交
,交![]() 于点
于点![]() (使用直尺和圆规,不写作法,保留作图痕迹);
(使用直尺和圆规,不写作法,保留作图痕迹);
(2)若![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.
科目:初中数学 来源: 题型:
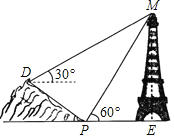
【题目】小明同学在综合实践活动中对本地的一座古塔进行了测量.如图,他在山坡坡脚P处测得古塔顶端M的仰角为60°,沿山坡向上走25m到达D处,测得古塔顶端M的仰角为30°.已知山坡坡度i=3:4,即tanθ=![]() ,请你帮助小明计算古塔的高度ME.(结果保留根号)
,请你帮助小明计算古塔的高度ME.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正比例函数y=2x和反比例函数的图象交于点A(m,﹣2).

(1)求反比例函数的解析式;
(2)观察图象,直接写出正比例函数值大于反比例函数值时自变量x的取值范围;
(3)若双曲线上点C(2,n)沿OA方向平移![]() 个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
个单位长度得到点B,判断四边形OABC的形状并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】工匠制作某种金属工具要进行材料煅烧和锻造两个工序,即需要将材料烧到800℃,然后停止煅烧进行锻造操作,经过8min时,材料温度降为600℃.煅烧时温度y(℃)与时间x(min)成一次函数关系;锻造时,温度y(℃)与时间x(min)成反比例函数关系(如图).已知该材料初始温度是32℃.
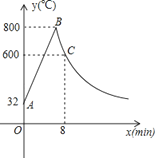
(1)分别求出材料煅烧和锻造时y与x的函数关系式,并且写出自变量x的取值范围;
(2)根据工艺要求,当材料温度低于480℃时,须停止操作.那么锻造的操作时间有多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接CD,过E作EF∥DC交BC的延长线于F.
(1)证明:四边形CDEF是平行四边形;
(2)若四边形CDEF的周长是25cm,AC的长为5cm,求线段AB的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC顶点的坐标分别为A(﹣3,3),B(﹣5,2),C(﹣1,1).
(1)以点C为位似中心,作出△ABC的位似图形△A1B1C,使其位似比为1:2,且ABC位于点C的异侧,并表示出点A1的坐标.
(2)作出△ABC绕点C顺时针旋转90°后的图形△A2B2C.
(3)在(2)的条件下求出点B经过的路径长(结果保留π).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】经过举国上下抗击新型冠状病毒的斗争,疫情得到了有效控制,国内各大企业在2月9日后纷纷进入复工状态.为了了解全国企业整体的复工情况,我们查找了截止到2020年3月1日全国部分省份的复工率,并对数据进行整理、描述和分析.下面给出了一些信息:
a.截止3月1日20时,全国已有11个省份工业企业复工率在90%以上,主要位于东南沿海地区,位居前三的分别是贵州(100%)、浙江(99.8%)、江苏(99%).
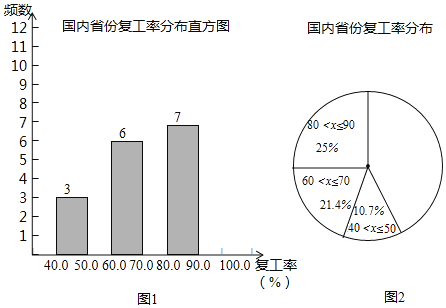
b.各省份复工率数据的频数分布直方图如图1(数据分成6组,分别是40<x≤50;
50<x≤60;60<x≤70;70<x≤80;80<x≤90;90<x≤100):
c.如图2,在b的基础上,画出扇形统计图:
d.截止到2020年3月1日各省份的复工率在80<x≤90这一组的数据是:
81.3 | 83.9 | 84 | 87.6 | 89.4 | 90 | 90 |
e.截止到2020年3月1日各省份的复工率的平均数、中位数、众数如下:
日期 | 平均数 | 中位数 | 众数 |
截止到2020年3月1日 | 80.79 | m | 50,90 |
请解答以下问题:
(1)依据题意,补全频数分布直方图;
(2)扇形统计图中50<x≤60这组的圆心角度数是 度(精确到0.1).
(3)中位数m的值是 .
(4)根据以上统计图表简述国内企业截止3月1日的复工率分布特征.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数y1=ax+b(a≠0)的图象与反比例函数y2=![]() (k≠0)的图象交于A、B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=4
(k≠0)的图象交于A、B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=4![]() ,cos∠ACH=
,cos∠ACH=![]() .
.
(1)求该反比例函数和一次函数的解析式;
(2)在x轴上是否存在点P,使三角形PAC是等腰三角形?若存在,请求出P点坐标;不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com