
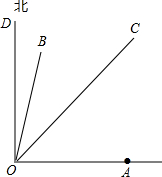
 如图,台风中心位于点O处,并沿东北方向(北偏东45°),以40千米/小时的速度匀速移动,在距离台风中心50千米的区域内会受到台风的影响,在点O的正东方向,距离60$\sqrt{2}$千米的地方有一城市A.
如图,台风中心位于点O处,并沿东北方向(北偏东45°),以40千米/小时的速度匀速移动,在距离台风中心50千米的区域内会受到台风的影响,在点O的正东方向,距离60$\sqrt{2}$千米的地方有一城市A.分析 (1)过点A作AH⊥OD于点H,可求得AH的长为60km,由60>50可知,不会受到台风影响;
(2)过点B作BG⊥OC于点G,可求得BG的长,由离台风中心50千米的区域内会受到台风的影响,即可知会受到影响,然后由勾股定理求得受影响的范围长,即可求得影响的时间.
解答 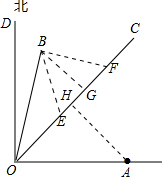 解:(1)作AH⊥OC,易知台风中心O与A市的最近距离为AD的长度,
解:(1)作AH⊥OC,易知台风中心O与A市的最近距离为AD的长度,
∵由题意得:∠HOA=45°,OA=60$\sqrt{2}$km,
∴AH=HO=60$\sqrt{2}$÷$\sqrt{2}$=60km,
∵60>50,
∴A市不会受到此台风的影响;
(2)作BG⊥OC于G,
∵由题意得:∠BOC=30°,OB=80km,
∴BG=$\frac{1}{2}$OB=40km,
∵40<50,
∴会受到影响,
如图:BE=BF=50km,由题意知,台风从E点开始影响B城市到F点影响结束,
∴EG=$\sqrt{B{E}^{2}-B{G}^{2}}$=30km,
∴EF=2EG=60km,
∵风速为40km/h,
∴60÷40=1.5小时,
∴影响时间约为1.5小时.
点评 此题考查了解直角三角形的应用-方向角问题以及勾股定理的应用.此题难度适中,注意掌握数形结合思想的应用,能从实际问题中整理出直角三角形是解答本题的关键.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
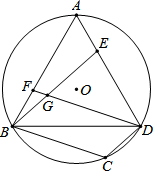 如图,已知△ABD为⊙O的内接正三角形,AB=2$\sqrt{7}$,E、F分别为边AD、AB上的动点,且AE=BF,DF与BE相交于G点,过B点作BC∥DF交$\widehat{BD}$于点C,连接CD.
如图,已知△ABD为⊙O的内接正三角形,AB=2$\sqrt{7}$,E、F分别为边AD、AB上的动点,且AE=BF,DF与BE相交于G点,过B点作BC∥DF交$\widehat{BD}$于点C,连接CD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
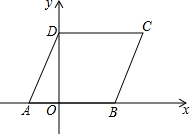 如图,在平面直角坐标系中,菱形ABCD的顶点A的坐标为(-3,0),∠DAB=60°,点B、D分别在x轴、y轴上,求点C的坐标及该菱形的面积.
如图,在平面直角坐标系中,菱形ABCD的顶点A的坐标为(-3,0),∠DAB=60°,点B、D分别在x轴、y轴上,求点C的坐标及该菱形的面积.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
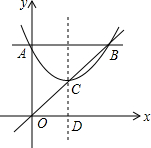 如图,抛物线y=$\frac{1}{3}$x2+bx+6与y轴相交于点A,与过点A且平行于x轴的直线相交于点B(点B在第一象限),抛物线的顶点C在直线OB上,平移直线OB,使平移后的直线OB与抛物线只有一个交点,则直线OB向右平移了$\frac{3}{4}$个单位.
如图,抛物线y=$\frac{1}{3}$x2+bx+6与y轴相交于点A,与过点A且平行于x轴的直线相交于点B(点B在第一象限),抛物线的顶点C在直线OB上,平移直线OB,使平移后的直线OB与抛物线只有一个交点,则直线OB向右平移了$\frac{3}{4}$个单位.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com