
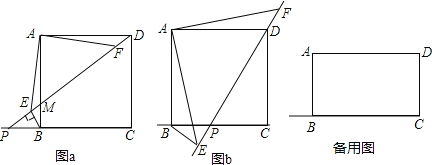
【题目】如图,正方形ABCD,点P在射线CB上运动(不包含点B、C),连接DP,交AB于点M,作BE⊥DP于点E,连接AE,作∠FAD=∠EAB,FA交DP于点F.
(1)如图a,当点P在CB的延长线上时,
①求证:DF=BE;
②请判断DE、BE、AE之间的数量关系并证明;
(2)如图b,当点P在线段BC上时,DE、BE、AE之间有怎样的数量关系?请直接写出答案,不必证明;
(3)如果将已知中的正方形ABCD换成矩形ABCD,且AD:AB=![]() :1,其他条件不变,当点P在射线CB上时,DE、BE、AE之间又有怎样的数量关系?请直接写出答案,不必证明.
:1,其他条件不变,当点P在射线CB上时,DE、BE、AE之间又有怎样的数量关系?请直接写出答案,不必证明.
【答案】(1)详见解析;②DE=BE+![]() AE,理由详见解析;(2)DE=
AE,理由详见解析;(2)DE=![]() AE﹣BE;(3)DE=2AE+
AE﹣BE;(3)DE=2AE+![]() BE或DE=2AE﹣
BE或DE=2AE﹣![]() BE.
BE.
【解析】
(1)①由正方形的性质得到AD=AB,∠BAD=90°,判断出△ABE≌△ADF,即可;②由①得到△ABE≌△ADF,并且判断出△EAF为直角三角形,用勾股定理即可;
(2)先由正方形的性质和已知条件判断出△ABE≌△ADF,再用判断出△EAF为直角三角形,用勾股定理即可;
(3)分两种情况讨论,先由正方形的性质和已知条件判断出△ABE∽△ADF,AF=![]() AE,DF=
AE,DF=![]() BE,再判断出△EAF为直角三角形,用勾股定理结合图形可得结论.
BE,再判断出△EAF为直角三角形,用勾股定理结合图形可得结论.
证明:(1)①正方形ABCD中,AD=AB,∠ADM+∠AMD=90°
∵BE⊥DP,
∴∠EBM+∠BME=90°,
∵∠AMD=∠BME,
∴∠EBM=∠ADM,
在△ABE和△ADF中,
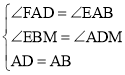 ,
,
∴△ABE≌△ADF,
∴DF=BE;
②DE=BE+![]() AE,
AE,
理由:由(1)有△ABE≌△ADF,
∴AE=AF,∠BAE=∠DAF,
∴∠BAE+∠FAM=∠DAF+∠FAM,
∴∠EAF=∠BAD=90°,
∴EF=![]() AE,
AE,
∵DE=DF+EF,
∴DE=BE+![]() AE;
AE;
(2)DE=![]() AE﹣BE;
AE﹣BE;
理由:正方形ABCD中,AD=AB,∠BAD=∠BAE+∠DAE=90°,
∵∠FAD=∠EAB,
∴∠EAF=∠BAD=90°,
∴∠AFE+∠AEF=90°
∵BE⊥DP,
∴∠BEA+∠AEF=90°,
∴∠BEA=∠AFE,
∵∠FAD=∠EAB,AD=AB
∴△ABE≌△ADF,
∴AE=AF,BE=DF
∵∠EAF=90°
∴EF=![]() AE,
AE,
∵EF=DF+DE=![]() AE,
AE,
∴DE=![]() AE﹣DF=
AE﹣DF=![]() AE﹣BE;
AE﹣BE;
(3)DE=2AE+![]() BE或DE=2AE﹣
BE或DE=2AE﹣![]() BE.
BE.
①如图1所示时,
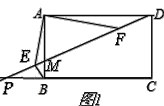
正方形ABCD中,∠ADM+∠AMD=90°
∵BE⊥DP,
∴∠EBM+∠BME=90°,
∵∠AMD=∠BME,
∴∠EBM=∠ADM,
∵∠FAD=∠EAB
∴△ABE∽△ADF,
∴![]() ,
,
∵AD:AB=![]() :1,
:1,
∴![]() ,
,
∴AF=![]() AE,DF=
AE,DF=![]() BE
BE
∵∠FAD=∠EAB
∴∠EAF=∠EAB+∠BAF=∠FAD+∠BAF=∠BAD=90°,
∴EF=![]() =2AE=DE﹣DF=DE﹣
=2AE=DE﹣DF=DE﹣![]() BE,
BE,
即:DE=2AE+![]() BE;
BE;
②如图2所示,
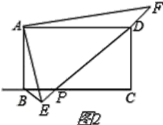
∵∠DAF=∠BAE,
∴∠EAF=∠BAD=90°,
∵∠DAF=∠BAE,
∴△BAE∽△DAF,
∴![]() ,
,
∵AD:AB=![]() :1,
:1,
∴![]() ,
,
∴AF=![]() AE,DF=
AE,DF=![]() BE,
BE,
∵∠EAF=90°,
根据勾股定理得,EF=![]() =2AE=DE+DF=DE+
=2AE=DE+DF=DE+![]() BE,
BE,
∴DE=2AE﹣![]() BE.
BE.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在△ABC中,AC=4,BC=2,点D在射线AB上,在构成的图形中,△ACD为等腰三角形,且存在两个互为相似的三角形,则CD的长是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE上的一点,使CF∥BD.

(1)求证:BE=CE;
(2)试判断四边形BFCD的形状,并说明理由;
(3)若BC=8,AD=10,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:
①4ac<b2;
②方程![]() 的两个根是x1=﹣1,x2=3;
的两个根是x1=﹣1,x2=3;
③3a+c>0
④当y>0时,x的取值范围是﹣1≤x<3
⑤当x<0时,y随x增大而增大
其中结论正确的个数是( )

A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,E为矩形ABCD的边AD上一点,点P从点B出发沿折线BE-ED-DC运动到点C停止,点Q从点B出发沿BC运动到点C停止,它们运动的速度都是1cm/s.若点P、点Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(![]() ),已知y与t之间的函数图象如图2所示.
),已知y与t之间的函数图象如图2所示.
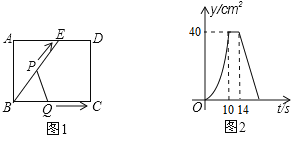
给出下列结论:①当0<t≤10时,△BPQ是等腰三角形;②![]() =48
=48![]() ;③当14<t<22时,y=110-5t;④在运动过程中,使得△ABP是等腰三角形的P点一共有3个;⑤△BPQ与△ABE相似时,t=14.5.
;③当14<t<22时,y=110-5t;④在运动过程中,使得△ABP是等腰三角形的P点一共有3个;⑤△BPQ与△ABE相似时,t=14.5.
其中正确结论的序号是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
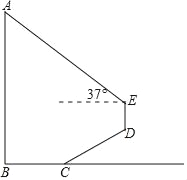
【题目】如图,为测量学校旗杆AB的高度,小明从旗杆正前方3米处的点C出发,沿坡度为i=1:![]() 的斜坡CD前进2
的斜坡CD前进2![]() 米到达点D,在点D处放置测角仪,测得旗杆顶部A的仰角为37°,量得测角仪DE的高为1.5米.A、B、C、D、E在同一平面内,且旗杆和测角仪都与地面垂直.
米到达点D,在点D处放置测角仪,测得旗杆顶部A的仰角为37°,量得测角仪DE的高为1.5米.A、B、C、D、E在同一平面内,且旗杆和测角仪都与地面垂直.
(1)求点D的铅垂高度(结果保留根号);
(2)求旗杆AB的高度(精确到0.1).
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75,![]() ≈1.73.)
≈1.73.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国农村劳动力人数有4.8亿.从目前来看,我国农民的科技水平还不高,在农村4.8亿的劳动力中,小学文化程度以下的占40%,具有初中文化程度的占48%,具有高中文化程度的占12%,受过职业技术培训的占5%,但据专家统计,他们中八成以上会进行分数、平均数、增长率等基本数学运算,能基本适应当代经济生活,这是初等数学教育的一大成就.
请根据上面的数据信息解答下列问题:
文化程度 | 人数(亿) | 会基本数学运算人数(亿) | 百分比 |
小学以下 | 1.4976 | ||
初中文化 | 2.0736 | 90% | |
高中文化 | 95% | ||
受过职业技术培训 | 0.2328 | 97% |
(1)填写下列农民受教育情况及掌握基本数学运算情况统计
(2)根据图表,求出农村劳动力中会进行基本数学运算的总人数占农村劳动力总人数的百分比;
(3)政府计划两年后使农村劳动力初、高中文化程度达到80%,那么平均每年增长的百分率是多少(精确到0.1%)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图1是一款优雅且稳定的抛物线型落地灯.防滑螺母C为抛物线支架的最高点,灯罩D距离地面1.86米,灯柱AB及支架的相关数据如图2所示.若茶几摆放在灯罩的正下方,则茶几到灯柱的距离AE为________米.
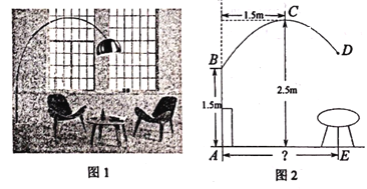
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD为⊙O的直径,AC为⊙O的弦,AB=AC,AD交BC于点E,AE=2,ED=4,延长DB到点F,使得BF=BO,连接FA.则下列结论中不正确的是( )

A. △ABE∽△ADBB. ∠ABC=∠ADB
C. AB=3![]() D. 直线FA与⊙O相切
D. 直线FA与⊙O相切
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com