
【题目】如图1,E为矩形ABCD的边AD上一点,点P从点B出发沿折线BE-ED-DC运动到点C停止,点Q从点B出发沿BC运动到点C停止,它们运动的速度都是1cm/s.若点P、点Q同时开始运动,设运动时间为t(s),△BPQ的面积为y(![]() ),已知y与t之间的函数图象如图2所示.
),已知y与t之间的函数图象如图2所示.
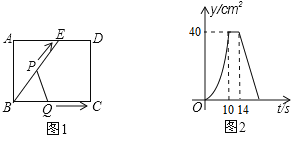
给出下列结论:①当0<t≤10时,△BPQ是等腰三角形;②![]() =48
=48![]() ;③当14<t<22时,y=110-5t;④在运动过程中,使得△ABP是等腰三角形的P点一共有3个;⑤△BPQ与△ABE相似时,t=14.5.
;③当14<t<22时,y=110-5t;④在运动过程中,使得△ABP是等腰三角形的P点一共有3个;⑤△BPQ与△ABE相似时,t=14.5.
其中正确结论的序号是_______.
【答案】①③⑤.
【解析】解:由图象可以判定:BE=BC=10 cm.DE=4 cm,当点P在ED上运动时,S△BPQ=![]() BCAB=40cm2,∴AB=8 cm,∴AE=6 cm,∴当0<t≤10时,点P在BE上运动,BP=BQ,∴△BPQ是等腰三角形,故①正确;
BCAB=40cm2,∴AB=8 cm,∴AE=6 cm,∴当0<t≤10时,点P在BE上运动,BP=BQ,∴△BPQ是等腰三角形,故①正确;
S△ABE=![]() ABAE=24 cm2,故②错误;
ABAE=24 cm2,故②错误;
当14<t<22时,点P在CD上运动,该段函数图象经过(14,40)和(22,0)两点,解析式为y=110﹣5t,故③正确;
△ABP为等腰直角三角形需要分类讨论:当AB=AP时,ED上存在一个符号题意的P点,当BA=BO时,BE上存在一个符合同意的P点,当PA=PB时,点P在AB垂直平分线上,所以BE和CD上各存在一个符号题意的P点,共有4个点满足题意,故④错误;
⑤△BPQ与△ABE相似时,只有;△BPQ∽△BEA这种情况,此时点Q与点C重合,即![]() ,∴PC=7.5,即t=14.5.
,∴PC=7.5,即t=14.5.
故⑤正确.
综上所述,正确的结论的序号是①③⑤.
故答案为:①③⑤.


科目:初中数学 来源: 题型:
【题目】某水果批发商经营甲、乙两种水果,根据以往经验和市场行情,预计夏季某一段时间内,甲种水果的销售利润![]() (万元)与进货量x(吨)近似满足函数关系
(万元)与进货量x(吨)近似满足函数关系![]() ,乙种水果的销售利润
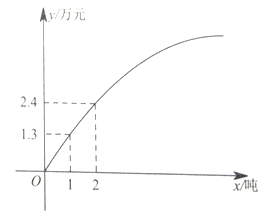
,乙种水果的销售利润![]() (万元)与进货量x(吨)之间的函数关系如图所示.
(万元)与进货量x(吨)之间的函数关系如图所示.
(1)求![]() (万元)与x(吨)之间的函数关系式;
(万元)与x(吨)之间的函数关系式;
(2)如果该批发商准备进甲、乙两种水果共10吨,设乙种水果的进货量为t吨,请你求出这两种水果所获得的销售利润总和W(万元)与t(吨)之间的函数关系式.并求出这两种水果各进多少吨时获得的销售利润总和最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
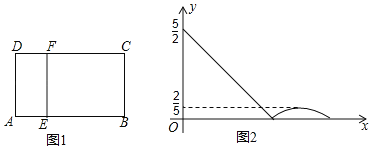
【题目】如图1,在矩形ABCD中,动点E从A出发,沿AB→BC方向运动,当点E到达点C时停止运动,过点E做FE⊥AE,交CD于F点,设点E运动路程为x,FC=y,如图2所表示的是y与x的函数关系的大致图象,当点E在BC上运动时,FC的最大长度是![]() ,则矩形ABCD的面积是( )
,则矩形ABCD的面积是( )
A. ![]() B. 5C. 6D.
B. 5C. 6D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高节水意识,小申随机统计了自己家7天的用水量,并分析了第3天的用水情况,将得到的数据进行整理后,绘制成如图所示的统计图.(单位:升)
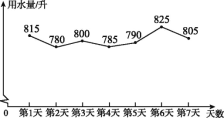
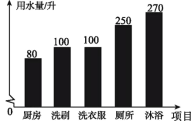
(1)求这7天内小申家每天用水量的平均数和中位数;
(2)求第3天小申家洗衣服的水占这一天总用水量的百分比;
(3)请你根据统计图中的信息,给小申家提出一条全理的节约用水建议,并估算采用你的建议后小申家一个月(按30天计算)的节约用水量.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学兴趣小组的活动中,小明进行数学探究活动,将边长为2的正方形ABCD与边长为2![]() 的正方形AEFG按图①位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
的正方形AEFG按图①位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
⑴小明发现DG⊥BE,请你帮他说明理由.
⑵如图②,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
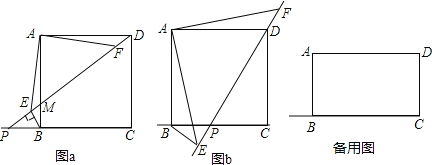
【题目】如图,正方形ABCD,点P在射线CB上运动(不包含点B、C),连接DP,交AB于点M,作BE⊥DP于点E,连接AE,作∠FAD=∠EAB,FA交DP于点F.
(1)如图a,当点P在CB的延长线上时,
①求证:DF=BE;
②请判断DE、BE、AE之间的数量关系并证明;
(2)如图b,当点P在线段BC上时,DE、BE、AE之间有怎样的数量关系?请直接写出答案,不必证明;
(3)如果将已知中的正方形ABCD换成矩形ABCD,且AD:AB=![]() :1,其他条件不变,当点P在射线CB上时,DE、BE、AE之间又有怎样的数量关系?请直接写出答案,不必证明.
:1,其他条件不变,当点P在射线CB上时,DE、BE、AE之间又有怎样的数量关系?请直接写出答案,不必证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品的进价为每件50元.当售价为每件70元时,每星期可卖出300件,现需降价处理,且经市场调查:每降价1元,每星期可多卖出20件.在确保盈利的前提下,解答下列问题:
(1)若设每件降价x元、每星期售出商品的利润为y元,请写出y与x的函数关系式,并求出自变量x的取值范围;
(2)当降价多少元时,每星期的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小雨、小华、小星暑假到某超市参加社会实践活动,在活动中他们参加了某种水果的销售工作,已知该水果的进价为8元/千克.他们通过市场调查发现:当销售单价为10元时,那么每天可售出300千克;销售单价每上涨1元,每天的销售量就减少50千克.
(1)求该超市销售这种水果,每天的销售量y(千克)与销售单价x(元/千克)之间的函数关系式;
(2)一段时间后,发现这种水果每天的销售量均不低于250千克,则此时该超市销售这种水果每天获取的利润w(元)最大是多少?
(3)为响应政府号召,该超市决定在暑假期间每销售1千克这种水果就捐赠a元利润(a≤2.5)给希望工程.公司通过销售记录发现,当销售单价不超过13元时,每天扣除捐赠后的日销售利润随销售单价x(元/千克)的增大而增大,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走9m到达B点,测得杆顶端点P和杆底端点Q的仰角分别是60°和30°.
(1)求∠BPQ的度数;
(2)求该电线杆PQ的高度.(结果保留根号)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com