
【题目】定义:P、Q分别是两条线段a和b上任意一点,线段PQ的长度的最小值叫做线段a与线段b的距离.
已知O(0,0),A(4,0),B(m,n),C(m+4,n)是平面直角坐标系中四点.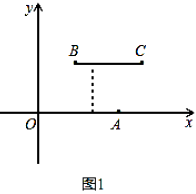
(1)根据上述定义,当m=2,n=2时,如图1,线段BC与线段OA的距离是;当m=5,n=2时,如图2,线段BC与线段OA的距离为;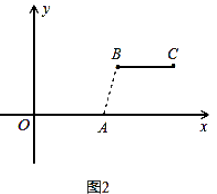
(2)如图3,若点B落在圆心为A,半径为2的圆上,线段BC与线段OA的距离记为d,求d关于m的函数解析式.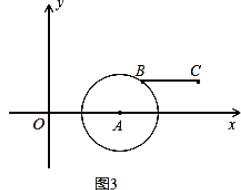
(3)当m的值变化时,动线段BC与线段OA的距离始终为2,线段BC的中点为M,
①求出点M随线段BC运动所围成的封闭图形的周长;
②点D的坐标为(0,2),m≥0,n≥0,作MH⊥x轴,垂足为H,是否存在m的值使以A、M、H为顶点的三角形与△AOD相似?若存在,求出m的值;若不存在,请说明理由.
【答案】
(1)2,![]()
(2)解:如图,
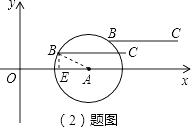
当点B落在⊙A上时,m的取值范围为2≤m≤6:
①当2≤m<4时,d=|n|(-2≤n≤2),
或:过点B作BE⊥x轴于点E,线段BC与线段OA的距离等于BE长,
OE=m,AE=OA-OE=4-m,
在Rt△ABE中,根据勾股定理得,d= ![]() =
= ![]() ;
;
②当4≤m≤6,显然线段BC与线段OA的距离等于⊙A半径,即d=2
(3)解:根据题意画出图形,点M形成的图形为图中红线表示的封闭图形,
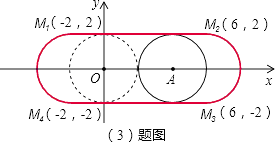
由图可见,封闭图形由上下两段长度为8的线段,以及左右两侧半径为2的半圆所组成,
其周长为:2×8+2×π×2=16+4π,
∴点M随线段BC运动所围成的封闭图形的周长为:16+4π
①先根据题意画出图形,易求出点M随线段BC运动所围成的封闭图形的周长;②
【解析】解:(1)当m=2,n=2时,线段BC与线段OA的距离等于平行线间的距离,即为2;当m=5,n=2时,B点坐标为(5,2),线段BC与线段OA的距离,即为线段AB的长,
如图,
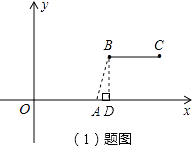
过点B作BD⊥x轴于点D,则AD=5-4=1,BD=2,
在Rt△ABD中,由勾股定理得:AB= ![]() ;
;
(1)按照新定义的要求可知当m=2,n=2时,线段BC与线段OA的距离等于平行线间的距离(为2),当m=5,n=2时,可求出点B的坐标,线段BC与线段OA的距离,即为线段AB的长,根据勾股定理就可求出结果。
(2)根据题意可知,当点B落在⊙A上时,m的取值范围为2≤m≤6:当①当2≤m<4时,过点B作BE⊥x轴于点E,线段BC与线段OA的距离等于BE长;②当4≤m≤6,显然线段BC与线段OA的距离等于⊙A半径,即d=2。
(3)先画出图形,符合题意的相似三角形有三个,再分类讨论,分别利用点的坐标关系及相似三角形的性质列出方程,即可求出m的值。


科目:初中数学 来源: 题型:
【题目】阅读与思考:
整式乘法与因式分解是方向相反的变形,由![]()
![]() ,
,
可得 ![]() .
.
利用这个式子可以将某些二次项系数是1的二次三项式分解因式.
例如:将式子![]() 分解因式.
分解因式.
这个式子的常数项![]() ,一次项系
,一次项系![]() ,
,
所以![]() .
.

解:![]()
![]() .
.
上述分解因式![]() 的过程,也可以用十字相乘的形式形象地表示:先分解二次项系数,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求代数和,使其等于一次项系数(如右图).
的过程,也可以用十字相乘的形式形象地表示:先分解二次项系数,分别写在十字交叉线的左上角和左下角;再分解常数项,分别写在十字交叉线的右上角和右下角;然后交叉相乘,求代数和,使其等于一次项系数(如右图).
请仿照上面的方法,解答下列问题:
(1)分解因式:![]() =___________________;
=___________________;
(2)若![]() 可分解为两个一次因式的积,则整数P的所有可能值是________.
可分解为两个一次因式的积,则整数P的所有可能值是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
∵![]() ,
,![]() ,
,![]() ,……
,……![]() ,
,
∴![]()
=![]()
=![]() =
=![]() .
.
解答下列问题:
(1)在和式![]() 中,第6项为______,第n项是__________.
中,第6项为______,第n项是__________.
(2)上述求和的想法是通过逆用分式减法法则,将和式中的各分数转化为两个数之差,使得除首末两项外的中间各项的和为_______,从而达到求和的目的.
(3)受此启发,请你解下面的方程:
![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明到某服装商场进行社会调查,了解到该商场为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法,并获得如下信息:
营业员 | 小丽 | 小华 |
月销售件数(件) | 200 | 150 |
月总收入(元) | 1400 | 1250 |
假设营业员的月基本工资为x元,销售每件服装奖励y元.
(1)求x、y的值;
(2)若营业员小丽某月的总收入不低于1800元,那么小丽当月至少要卖服装多少件?
(3)商场为了多销售服装,对顾客推荐一种购买方式:如果购买甲3件,乙2件,丙1件共需315元;如果购买甲1件,乙2件,丙3件共需285元.某顾客想购买甲、乙、丙各一件共需 元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD是△ABC的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.
(1)请判断四边形EBGD的形状,并说明理由;
(2)若∠ABC=30°,∠C=45°,ED=2![]() ,点H是BD上的一个动点,求HG+HC的最小值.
,点H是BD上的一个动点,求HG+HC的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
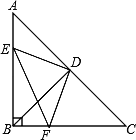
【题目】已知:如图,在△ABC中,∠ABC=90°,AB=BC,D是AC的中点,点E在AC上,点F在BC上,且AE=BF.
(1)求证:DE=DF;
(2)连接EF,求∠DEF的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com