
【题目】(2016·西宁中考)如图,D为⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD.
(1)求证:CD是⊙O的切线;
(2)过点B作⊙O的切线交CD的延长线于点E,BC=6, ![]() ,求BE的长.
,求BE的长.

【答案】(1)见解析 (2)![]()
(1)证明:连接OD.∵OB=OD,∴∠OBD=∠BDO.∵∠CDA=∠CBD,∴∠CDA=∠ODB.又∵AB是⊙O的直径,∴∠ADB=90°,∴∠ADO+∠ODB=90°,∴∠ADO+∠CDA=90°,即∠CDO=90°,∴OD⊥CD.∵OD是⊙O的半径,∴CD是⊙O的切线;
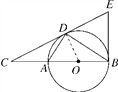
(2)解:∵∠C=∠C,∠CDA=∠CBD,∴△CDA∽△CBD,∴![]() =
=![]() .∵
.∵![]() =
=![]() ,BC=6,∴CD=4.∵CE,BE是⊙O的切线,∴BE=DE,BE⊥BC,∴BE2+BC2=EC2,即BE2+62=(4+BE)2,解得BE=
,BC=6,∴CD=4.∵CE,BE是⊙O的切线,∴BE=DE,BE⊥BC,∴BE2+BC2=EC2,即BE2+62=(4+BE)2,解得BE=![]() .
.
【解析】试题分析:连接OD.根据圆周角定理得到∠ADO+∠ODB=90°,
而∠CDA=∠CBD,∠CBD=∠BDO.于是∠ADO+∠CDA=90°,可以证明是切线.
![]() 根据已知条件得到
根据已知条件得到![]() 由相似三角形的性质得到
由相似三角形的性质得到![]() 求得
求得![]() 由切线的性质得到
由切线的性质得到![]() 根据勾股定理列方程即可得到结论.
根据勾股定理列方程即可得到结论.
试题解析:(1)连接OD.
∵OB=OD,
∴∠OBD=∠BDO.
∵∠CDA=∠CBD,
∴∠CDA=∠ODB.
又∵AB是⊙O的直径,∴∠ADB=90°,
∴∠ADO+∠ODB=90°,
∴∠ADO+∠CDA=90°,即∠CDO=90°,
∴OD⊥CD.
∵OD是⊙O的半径,
∴CD是⊙O的切线;
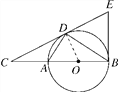
(2)∵∠C=∠C,∠CDA=∠CBD,∴△CDA∽△CBD,
![]()
![]() BC=6,∴CD=4.
BC=6,∴CD=4.
∵CE,BE是⊙O的切线,
∴BE=DE,BE⊥BC,
∴BE2+BC2=EC2,
即BE2+62=(4+BE)2,
解得BE=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=3,BC=4.将边AC沿CE翻折,使点A落在AB上的点D处;再将边BC沿CF翻折,使点B落在CD的延长线上的点B′处,两条折痕与斜边AB分别交于点E、F,则线段B′F的长为( )
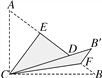
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2-2![]() x+m=0有两个不相等的实数根.
x+m=0有两个不相等的实数根.
(1)求实数m的最大整数值;
(2)在(1)的条件下,方程的实数根是x1,x2,求代数式![]() +
+![]() -
-![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】气象台预报“本市明天降水概率是85%”,对此信息,下列说法正确的是( )
A.本市明天将有85%的地区降水 B.本市明天将有85%的时间降水
C.明天降水的可能性比较大 D.明天肯定下雨
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】规定一种新运算:a△b=ab﹣a+b+1,如3△4=34﹣3+4+1,请比较大小:(﹣3)△4_____4△(﹣3)(填“>”、“=”或“<”)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com