
【题目】已知AB是⊙O的直径,弦CD与AB相交,∠BAC=38°.
(1)如图①,若D为弧AB的中点,求∠ABC和∠ABD的大小;
(2)如图②,过点D作⊙O的切线,与AB的延长线交于点P,若DP∥AC,求∠OCD的大小.
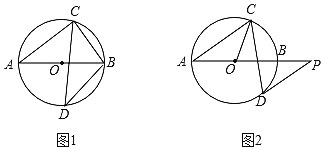
【答案】(1)∠ABC=52°,∠ABD=45°;(2)∠OCD=26°.
【解析】
(1)根据圆周角和圆心角的关系和图形可以求得∠ABC和∠ABD的大小;
(2)根据题意和平行线的性质、切线的性质可以求得∠OCD的大小.
(1)∵AB是⊙O的直径,弦CD与AB相交,∠BAC=38°,∴∠ACB=90°,∴∠ABC=∠ACB﹣∠BAC=90°﹣38°=52°.
∵D为![]() 的中点,∠AOB=180°,∴∠AOD=90°,∴∠ABD=45°;
的中点,∠AOB=180°,∴∠AOD=90°,∴∠ABD=45°;
(2)连接OD.
∵DP切⊙O于点D,∴OD⊥DP,即∠ODP=90°,由DP∥AC,又∠BAC=38°,∴∠P=∠BAC=38°.
∵∠AOD是△ODP的一个外角,∴∠AOD=∠P+∠ODP=128°,∴∠ACD=64°.
∵OC=OA,∠BAC=38°,∴∠OCA=∠BAC=38°,∴∠OCD=∠ACD﹣∠OCA=64°﹣38°=26°.


 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
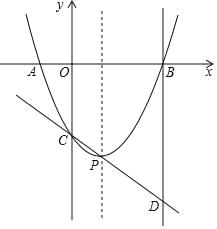
【题目】如图,二次函数 y=ax2﹣2ax+c(a>0)的图象与 x 轴的负半轴和正半轴分别交于 A、B 两点,与 y 轴交于点 C,它的顶点为 P,直线 CP 与过点B 且垂直于 x 轴的直线交于点 D,且 CP:PD=1:2,tan∠PDB=![]() .
.
(1)则 A、B 两点的坐标分别为 A( , ); B( , );
(2)求这个二次函数的解析式;
(3)在抛物线的对称轴上找一点M 使|MC﹣MB|的值最大,则点M 的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P为△ABC的内心,延长AP交△ABC的外接圆⊙O于D,过D作DE∥BC,交AC的延长线于E点.①则直线DE与⊙O的位置关系是_____;②若AB=4,AD=6,CE=3,则DE=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】韦达定理:若一元二次方程ax2+bx+c=0(a≠0)的两根分别为x1、x2 , 则x1+x2=﹣![]() , x1x2=
, x1x2=![]() , 阅读下面应用韦达定理的过程:
, 阅读下面应用韦达定理的过程:
若一元二次方程﹣2x2+4x+1=0的两根分别为x1、x2 , 求x12+x22的值.
解:该一元二次方程的△=b2﹣4ac=42﹣4×(﹣2)×1=24>0
由韦达定理可得,x1+x2=﹣![]() =﹣
=﹣![]() =2,x1x2=
=2,x1x2=![]() =
=![]() =﹣
=﹣![]()
x12+x22=(x1+x2)2﹣2x1x2
=22﹣2×(﹣![]() )
)
=5
然后解答下列问题:
(1)设一元二次方程2x2+3x﹣1=0的两根分别为x1,x2, 不解方程,求x12+x22的值;
(2)若关于x的一元二次方程(k﹣1)x2+(k2﹣1)x+(k﹣1)2=0的两根分别为α,β,且α2+β2=4,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
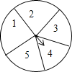
【题目】如图,有一个可以自由转动的转盘,被均匀分成![]() 等份,分别标上
等份,分别标上![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五个数字.甲乙两人玩一个游戏,其规则如下:任意转动转盘一次,转盘停止后,指针指向一个数字,如果所得的数字是偶数,则甲胜;如果所得的数字是奇数,则乙胜.
五个数字.甲乙两人玩一个游戏,其规则如下:任意转动转盘一次,转盘停止后,指针指向一个数字,如果所得的数字是偶数,则甲胜;如果所得的数字是奇数,则乙胜.
(1)转出的数字是![]() 的概率是________
的概率是________
(2)转出的数字不大于![]() 的概率是________
的概率是________
(3)转出的数字是偶数的概率是________
(4)你认为这样的游戏规则对甲、乙两人是否公平?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店分两次购进![]() 、
、![]() 两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
购进数量 | 购进所需费用(元) | ||
|
| ||
第一次 | 30 | 40 | 3800 |
第二次 | 40 | 30 | 3200 |
(1)求![]() 、
、![]() 两种商品每件的进价分别是多少元?
两种商品每件的进价分别是多少元?
(2)商场决定![]() 种商品以每件30元出售,
种商品以每件30元出售,![]() 种商品以每件100元出售.为满足市场需求,需购进
种商品以每件100元出售.为满足市场需求,需购进![]() 、
、![]() 两种商品共1000件,且
两种商品共1000件,且![]() 种商品的数量不少于
种商品的数量不少于![]() 种商品数量的4倍,设购进
种商品数量的4倍,设购进![]() 种商品
种商品![]() 件,获得的利润为
件,获得的利润为![]() 元,
元,
①请列出![]() 与
与![]() 的函数关系式
的函数关系式
②求出获利最大的进货方案,并确定最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.则下列结论:①△ABG≌△AFG②BG=CG③AG∥CF④S△FGC=3⑤∠AGB+∠AED=135°.其中正确的个数是( )
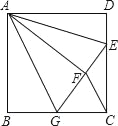
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.
(1)求证:△CDB≌△BAG.
(2)如果四边形BFDE是菱形,那么四边形AGBD是什么特殊四边形?并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分10分)如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() 为常数,且
为常数,且![]() )的图象交于A(1,a)、B两点.
)的图象交于A(1,a)、B两点.
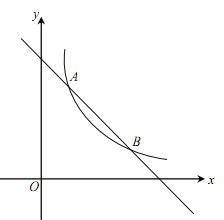
(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com