
����Ŀ��ij�̵�����ι���![]() ��
��![]() ������Ʒ�������ۣ����ι���ͬһ����Ʒ�Ľ�����ͬ������������±���ʾ��
������Ʒ�������ۣ����ι���ͬһ����Ʒ�Ľ�����ͬ������������±���ʾ��
�������� | ����������ã�Ԫ�� | ||
|
| ||
��һ�� | 30 | 40 | 3800 |
�ڶ��� | 40 | 30 | 3200 |
��1����![]() ��
��![]() ������Ʒÿ���Ľ��۷ֱ��Ƕ���Ԫ��
������Ʒÿ���Ľ��۷ֱ��Ƕ���Ԫ��
��2���̳�����![]() ����Ʒ��ÿ��30Ԫ���ۣ�
����Ʒ��ÿ��30Ԫ���ۣ�![]() ����Ʒ��ÿ��100Ԫ���ۣ�Ϊ�����г������蹺��
����Ʒ��ÿ��100Ԫ���ۣ�Ϊ�����г������蹺��![]() ��
��![]() ������Ʒ��1000������
������Ʒ��1000������![]() ����Ʒ������������
����Ʒ������������![]() ����Ʒ������4�����蹺��
����Ʒ������4�����蹺��![]() ����Ʒ
����Ʒ![]() ������õ�����Ϊ
������õ�����Ϊ![]() Ԫ��
Ԫ��
�����г�![]() ��
��![]() �ĺ�����ϵʽ
�ĺ�����ϵʽ
������������Ľ�����������ȷ���������
���𰸡���1��![]() ����Ʒÿ���Ľ���Ϊ20Ԫ��
����Ʒÿ���Ľ���Ϊ20Ԫ��![]() ����Ʒÿ���Ľ���Ϊ80Ԫ����2����
����Ʒÿ���Ľ���Ϊ80Ԫ����2����![]()
![]() ���ڹ���
���ڹ���![]() ����Ʒ800����
����Ʒ800����![]() ����Ʒ200��ʱ��������������������Ϊ12000Ԫ��
����Ʒ200��ʱ��������������������Ϊ12000Ԫ��
��������
��1�����ݱ����е����ݿ����г���Ӧ�Ķ�Ԫһ�η����飬�Ӷ��������A��B������Ʒÿ���Ľ��ۣ�
��2���ٸ���������Եõ��������A����Ʒ�����ĺ�����ϵ���ڸ���![]() ����Ʒ������������
����Ʒ������������![]() ����Ʒ������4�������Եõ�����A����Ʒ������ȡֵ��Χ���ٸ���һ�κ��������ʣ����ɵõ��������Ľ�����������ȷ���������
����Ʒ������4�������Եõ�����A����Ʒ������ȡֵ��Χ���ٸ���һ�κ��������ʣ����ɵõ��������Ľ�����������ȷ���������
�⣺��1����![]() ����Ʒÿ���Ľ���Ϊ
����Ʒÿ���Ľ���Ϊ![]() Ԫ��
Ԫ��![]() ����Ʒÿ���Ľ���Ϊ
����Ʒÿ���Ľ���Ϊ![]() Ԫ��
Ԫ��
��������ã�![]() ��
��
��ã�![]() ��
��
�� ��![]() ����Ʒÿ���Ľ���Ϊ20Ԫ��
����Ʒÿ���Ľ���Ϊ20Ԫ��![]() ����Ʒÿ���Ľ���Ϊ80Ԫ��
����Ʒÿ���Ľ���Ϊ80Ԫ��
��2�����蹺��![]() ����Ʒ
����Ʒ![]() ������õ�����Ϊ
������õ�����Ϊ![]() Ԫ����
Ԫ����![]() ����Ʒ
����Ʒ![]() ����
����
��������ã�![]()
�ڡ�![]() ����Ʒ������������
����Ʒ������������![]() ����Ʒ������4����
����Ʒ������4����
��![]() ��
��
��ã�![]() ��
��
����![]() ��
�У�
��![]()
��![]() ��ֵ��
��ֵ��![]() �����������
�����������
��![]() ʱ��
ʱ��![]() ȡ���ֵ�����ֵΪ
ȡ���ֵ�����ֵΪ![]() ��
��
������![]() ����Ʒ800����
����Ʒ800����![]() ����Ʒ200��ʱ��������������������Ϊ12000Ԫ��
����Ʒ200��ʱ��������������������Ϊ12000Ԫ��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
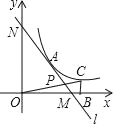
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��l��x���ཻ�ڵ�M��3��0������y���ཻ�ڵ�N��0��4������AΪMN���е㣬����������y=![]() ��x��0����ͼ�����A��
��x��0����ͼ�����A��
��1����ֱ��l�ͷ����������Ľ���ʽ��
��2���ں���y=![]() ��k��0����ͼ����ȡ���ڵ�A��һ��C����CB��x���ڵ�B������OC��ֱ��l�ڵ�P������ONP������ǡ�OBC�����3�������P�����꣮
��k��0����ͼ����ȡ���ڵ�A��һ��C����CB��x���ڵ�B������OC��ֱ��l�ڵ�P������ONP������ǡ�OBC�����3�������P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
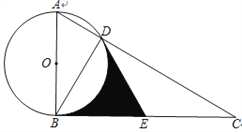
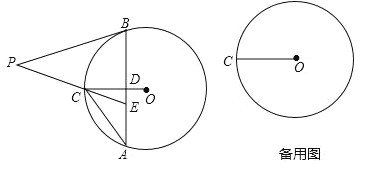
����Ŀ����ͼ��Rt��ABC�У���ABCΪֱ�ǣ���ABΪֱ������O��AC�ڵ�D����EΪBC�е㣬����DE��DB.
��1����֤��DE����O���У�
��2������C��30�㣬����BOD�Ķ�����
��3���ڣ�2���������£�����O�뾶Ϊ2�� ����Ӱ���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(9��)��֪��![]() ABCD������AB��AD�ij��ǹ���x�ķ���
ABCD������AB��AD�ij��ǹ���x�ķ���![]() ������ʵ������
������ʵ������
��1����mΪ��ֵʱ���ı���ABCD�����Σ������ʱ���εı߳���
��2����AB�ij�Ϊ2����ô![]() ABCD���ܳ��Ƕ��٣�
ABCD���ܳ��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪AB�ǡ�O��ֱ������CD��AB�ཻ����BAC=38����
��1����ͼ�٣���DΪ��AB���е㣬���ABC�͡�ABD�Ĵ�С��
��2����ͼ�ڣ�����D����O�����ߣ���AB���ӳ��߽��ڵ�P����DP��AC�����OCD�Ĵ�С��
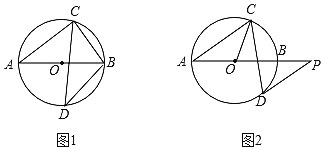
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ؽ�����Ϊ�˷ḻ����ѧ���Ĵ�μ���Ҫ���ѧУ��չ��ʽ�����������������ij��ѧ����ѧ���������Ȥ�����������⣬��������˱�Уij���ѧ���������ݵ��������Ƴ����µIJ�����������ͳ��ͼ������ͳ��ͼ��
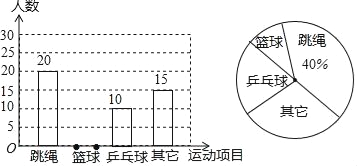
��1������ε����У�ϲ��������Ŀ��ͬѧ���� ���ˣ�������ͳ��ͼ�У���ƹ�������İٷֱ�Ϊ�� ��%�����ѧУ��800��ѧ��������ȫУѧ�������� ����ϲ��������Ŀ��
��2���뽫����ͳ��ͼ����������
��3���ڱ������ѧ���У�ϲ���������2��Ůͬѧ������Ϊ��ͬѧ����Ҫ���������ȡ2��ͬѧ�����༶�μ�У����ӣ���ֱ��д������ȡ��2��ͬѧǡ����1��Ůͬѧ��1����ͬѧ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ˮ�����Ű�����ÿ��4Ԫ�ļ۸�ij��ˮ�����ɽȻ����ÿ��6Ԫ�ļ۸���ۣ�ÿ����۳�150�ͨ�����鷢�֣�����ˮ��ÿ����ۼ�ÿ����0.1Ԫ��ÿ��ɶ��۳�30�Ϊ��֤ÿ�������۳�360��Ű��̾����������ۣ�
��1����������ˮ��ÿ����ۼ۽���xԪ����ÿ������������� ����ú�x�Ĵ���ʽ��ʾ����
��2����������ˮ��Ҫ��ÿ��ӯ��450Ԫ���Ű����轫ÿ����ۼ۽��Ͷ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����֪y=��m2+m��![]() +��m��3��x+m2��x�Ķ��κ�����������Ľ���ʽ��
+��m��3��x+m2��x�Ķ��κ�����������Ľ���ʽ��
��2�����䷽������κ���y=��x2+5x��7�Ķ������겢������������ֵ����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������O�����뾶OC��6��DΪ�뾶OC������O��C�ĵ�������D��AB��OC������O��A��B����E���߶�AB����AE��CE����P���߶�EC���ӳ�������PB��PE��
��1����OD��2������AB�ij���
��2������D���߶�OC�������˵������ƶ�ʱ��ֱ��PB����O��������λ�ù�ϵ����˵��������
��3����Q����O�ϵ�һ������������DΪOC�е�ʱ���߶�PQ����СֵΪ���٣���˵��������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com