
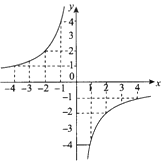
【题目】作出反比例函数y=-![]() 的图象,并结合图象回答:(1)当x=2时,y的值;(2)当1<x≤4时,y的取值范围;(3)当1≤y<4时,x的取值范围.
的图象,并结合图象回答:(1)当x=2时,y的值;(2)当1<x≤4时,y的取值范围;(3)当1≤y<4时,x的取值范围.
【答案】(1)y=-2;(2)y的取值范围为-4<y≤-1;(3)x的取值范围-4≤x<-1.
【解析】
列表,根据描点法画出图像即可;(1)把x=2代入反比例解析式求出y的值即可;(2)分别求出x=1与x=4时y的值,结合图象确定出y的范围即可;(3)分别求出y=1与y=4时x的值,结合图象确定出x的范围即可.
列表得:
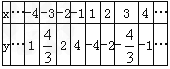
作出反比例y=-![]() 的图象,如图所示,
的图象,如图所示,
(1)把x=2代入,得y=-![]() =-2;
=-2;
(2)当x=1时,y=-4;当x=4时,y=-1,
根据图象,得当1<x≤4时,y的取值范围为-4<y≤-1;
(3)当y=1时,x=-4;当y=4时,x=-1,
根据题意,得当1≤y<4时,x的取值范围为-4≤x<-1.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某电商销售一款夏季时装,进价40元/件,售价110元/件,每天销售20件,每销售一件需缴纳电商平台推广费用a元(a>0)。未来30天,这款时装将开展“每天降价1元”的夏令促销活动,即从第1天起每天的单价均比前一天降1元。通过市场调研发现,该时装单价每降1元,每天销量增加4件。在这30天内,要使每天缴纳电商平台推广费用后的利润随天数t(t为正整数)的增大而增大,a的取值范围应为_____________。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 与反比例函数
与反比例函数![]() (
(![]() )的图象都经过点A(1,m).
)的图象都经过点A(1,m).
(1)求反比例函数的表达式;
(2)当二次函数与反比例函数的值都随x的增大而减小时,求x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
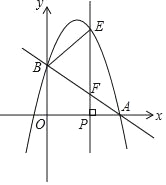
【题目】如图,在平面直角坐标系中,直线y=-![]() x+2分别交x轴、y轴于点A、B,抛物线y=﹣x2+bx+c经过点A、B.点P是x轴上一个动点,过点P作垂直于x轴的直线分别交抛物线和直线AB于点E和点F.设点P的横坐标为m.
x+2分别交x轴、y轴于点A、B,抛物线y=﹣x2+bx+c经过点A、B.点P是x轴上一个动点,过点P作垂直于x轴的直线分别交抛物线和直线AB于点E和点F.设点P的横坐标为m.
(1)点A的坐标为 .
(2)求这条抛物线所对应的函数表达式.
(3)点P在线段OA上时,若以B、E、F为顶点的三角形与△FPA相似,求m的值.
(4)若E、F、P三个点中恰有一点是其它两点所连线段的中点(三点重合除外),称E、F、P三点为“共谐点”.直接写出E、F、P三点成为“共谐点”时m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们,在我们进入高中以后,将还会学到下面三角函数公式:
sin (α-β)=sinαcosβ-cosαsinβ,
cos (α-β)=cosαcosβ+sinαsinβ
例:sin 15°=sin (45°-30°)=sin 45°cos 30°-cos 45°sin 30°=![]()
(1)试仿照例题,求出cos 15°的准确值;
(2)我们知道,tanα=![]() ,试求出tan 15°的准确值.
,试求出tan 15°的准确值.
查看答案和解析>>
科目:初中数学 来源: 题型:
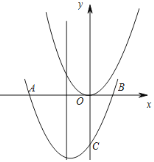
【题目】如图,在平面直角坐标系xOy中,将抛物线y=x2平移,使平移后的抛物线经过点A(–3,0)、B(1,0).
(1)求平移后的抛物线的表达式.
(2)设平移后的抛物线交y轴于点C,在平移后的抛物线的对称轴上有一动点P,当BP与CP之和最小时,P点坐标是多少?
(3)若y=x2与平移后的抛物线对称轴交于D点,那么,在平移后的抛物线的对称轴上,是否存在一点M,使得以M、O、D为顶点的三角形△BOD相似?若存在,求点M坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
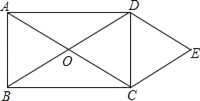
【题目】如图所示,O为矩形ABCD对角线的交点,DE∥AC,CE∥BD.
(1)试判断四边形OCED的形状,并说明理由;
(2)若AB=3,BC=4,求四边形OCED的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
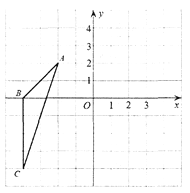
【题目】如图,在平面直角坐标系中,△ABC的顶点坐标分别为A(-2,2),B(-4,0),C(-4;-4),
(1)在y轴右侧,以O为位似中心,画出△A'B'C′,使它与△ABC的相似比为1:2;
(2)根据(1)的作图,sin∠A'C'B′=__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
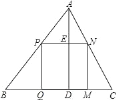
【题目】如图,△ABC是一块锐角三角形余料,边BC=120cm,高AD=80cm,要把它加工成一个矩形零件,使矩形PQMN的一边在BC上,其余两个顶点分别在AB、AC上.设PQ=xcm,矩形PQMN的面积为ycm2,请写出y关于x的函数表达式(并注明x的取值范围)_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com