
【题目】将一副三角尺如图拼接:含30°角的三角尺(△ABC)的长直角边与含45°角的三角尺(△ACD)的斜边恰好重合.已知AB= ![]() ,P是AC上的一个动点.
,P是AC上的一个动点. 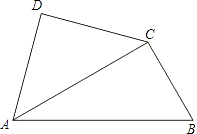
(1)当点P运动到∠ABC的平分线上时,连接DP,求DP的长;
(2)当点P在运动过程中出现PD=BC时,求此时∠PDA的度数;
(3)当点P运动到什么位置时,以D,P,B,Q为顶点的平行四边形的顶点Q恰好在边BC上?求出此时DPBQ的面积.
【答案】
(1)解:在Rt△ABC中,AB=2 ![]() ,∠BAC=30°,
,∠BAC=30°,
∴BC= ![]() ,AC=3.
,AC=3.
如图(1),作DF⊥AC.
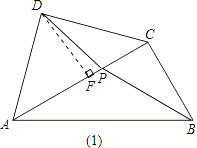
∵Rt△ACD中,AD=CD,
∴DF=AF=CF= ![]() .
.
∵BP平分∠ABC,
∴∠PBC=30°,
∴CP=BCtan30°=1,
∴PF= ![]() ,
,
∴DP= ![]() =
= ![]()
(2)解:当P点位置如图(2)所示时,
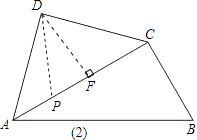
根据(1)中结论,DF= ![]() ,∠ADF=45°,
,∠ADF=45°,
又∵PD=BC= ![]() ,
,
∴cos∠PDF= ![]() =
= ![]() ,
,
∴∠PDF=30°.
∴∠PDA=∠ADF﹣∠PDF=15°.
当P点位置如图(3)所示时,
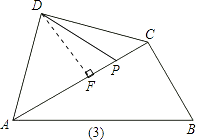
同(2)可得∠PDF=30°.
∴∠PDA=∠ADF+∠PDF=75°.
故∠PDA的度数为15°或75°;
(3)解:当点P运动到边AC中点(如图4),即CP= ![]() 时,
时,
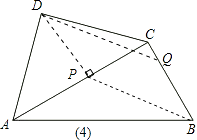
以D,P,B,Q为顶点的平行四边形的顶点Q恰好在边BC上.
∵四边形DPBQ为平行四边形,
∴BC∥DP,
∵∠ACB=90°,
∴∠DPC=90°,即DP⊥AC.
而在Rt△ABC中,AB=2 ![]() ,BC=
,BC= ![]() ,
,
∴根据勾股定理得:AC=3,
∵△DAC为等腰直角三角形,
∴DP=CP= ![]() AC=
AC= ![]() ,
,
∵BC∥DP,
∴PC是平行四边形DPBQ的高,
∴S平行四边形DPBQ=DPCP= ![]() .
.
【解析】(1)作DF⊥AC,由AB的长求得BC、AC的长.在等腰Rt△DAC中,DF=FA=FC;在Rt△BCP中,求得PC的长.则由勾股定理即可求得DP的长.(2)由(1)得BC与DF的关系,则DP与DF的关系也已知,先求得∠PDF的度数,则∠PDA的度数也可求出,需注意有两种情况.(3)由于四边形DPBQ为平行四边形,则BC∥DF,P为AC中点,作出平行四边形,求得面积.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,正方形OABC的面积为9,点O为坐标原点,点B在函数y=![]() (k>0,x>0)的图像上点P(m,n)是函数图像上任意一点,过点P分别作x轴y轴的垂线,垂足分别为E,F.并设矩形OEPF和正方形OABC不重合的部分的面积为S.
(k>0,x>0)的图像上点P(m,n)是函数图像上任意一点,过点P分别作x轴y轴的垂线,垂足分别为E,F.并设矩形OEPF和正方形OABC不重合的部分的面积为S.
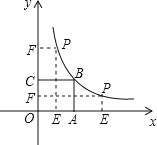
(1)求k的值;
(2)当S=![]() 时 求p点的坐标;
时 求p点的坐标;
(3)写出S关于m的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上有A、B、C、D四个整数点(即各点均表示整数),且3AB=BC=2CD.若A、D两点所表示的数分别是﹣6和5,则线段AC的中点所表示的数是( )
![]()
A. ﹣3 B. ﹣1 C. 3 D. ﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把弯曲的道路改直,就能缩短两点问的距离,其中蕴含的数学原理是( )
A. 两点确定一条直线B. 两点之间线段最短
C. 过一点有无数条直线D. 线段是直线的一部分
查看答案和解析>>
科目:初中数学 来源: 题型:
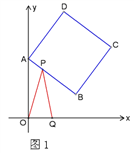
【题目】如图1,正方形 ABCD中,点A、B的坐标分别为(0,10),(8,4),点C在第一象限.动点P在正方形ABCD的边上,从点A出发沿A→B→C→D匀速运动,同时动点Q以相同速度在x轴上运动,当P点到D点时,两点同时停止运动,设运动的时间为t秒.
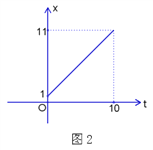
(1)当P点在边AB上运动时,点Q的横坐标![]() (长度单位)关于运动时间t(秒)的函数图象如图2所示,请写出点Q开始运动时的坐标及点P运动速度;
(长度单位)关于运动时间t(秒)的函数图象如图2所示,请写出点Q开始运动时的坐标及点P运动速度;
(2)求正方形边长及顶点C的坐标;
(3)在(1)中当t为何值时,△OPQ的面积最大,并求此时P点的坐标.
(4)如果点P、Q保持原速度速度不变,当点P沿A→B→C→D匀速运动时,OP与PQ能否相等,若能,写出所有符合条件的t的值;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com