
 在中超联赛期间,一队员在距离球门12米处挑射,正好射中了2.4米高的横梁,已知球的最高点距球门的水平距离为3米,若足球运行的路线是抛物线,如图,求其函数解析式.
在中超联赛期间,一队员在距离球门12米处挑射,正好射中了2.4米高的横梁,已知球的最高点距球门的水平距离为3米,若足球运行的路线是抛物线,如图,求其函数解析式. 分析 根据题意设函数解析式为y=a(x-3)2+k,代入点的坐标即可求得函数的解析式.
解答 解:∵球的最高点距球门的水平距离为3米,
∴设函数解析式为:y=a(x-3)2+k,
∴$\left\{\begin{array}{l}{0=a(12-3)^{2}+k}\\{2.4=a(0-3)^{2}+k}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a=-\frac{1}{30}}\\{k=\frac{7}{10}}\end{array}\right.$,
∴y=-$\frac{1}{30}$(x-3)2+$\frac{27}{10}$,
即函数解析式为:y=-$\frac{1}{30}$x2+$\frac{1}{5}$x+$\frac{12}{5}$.
点评 此题主要考查了二次函数的性质,根据题意得出图象上的点的坐标,进而得出方程组是解决问题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
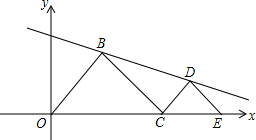 如图,E为(8,0),C是线段OE上一动点(不包括两个端点),分别以OC、CE为斜边,在第一象限作等腰Rt△OBC和等腰Rt△CDE,其中∠OBC=∠CDE=90°.设OC=a
如图,E为(8,0),C是线段OE上一动点(不包括两个端点),分别以OC、CE为斜边,在第一象限作等腰Rt△OBC和等腰Rt△CDE,其中∠OBC=∠CDE=90°.设OC=a查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com