
分析 根据平行公理、平移的性质和平行线的判定与性质进行判断即可.
解答 解:①在同一平面内,三条直线只有两个交点,则其中两条直线互相平行,正确;
②过直线外一点有且只有一条直线与已知直线平行,错误;
③平移过程中,各组对应点连成两条线段平行或者在同一直线上且相等,错误;
④两条直线与第三条直线相交,如果内错角相等,那么这两条直线平行,所以同旁内角互补,正确;
⑤两平行线被第三条直线所截得的同旁内角的平分线互相垂直,正确;
⑥如果甲看乙的方向是北偏东60°,那么乙看甲的方向是南偏西30°,错误;
⑦垂直于同一条直线的两条直线平行,必须是同一平面,故错误.
故答案为:4.
点评 本题考查了平行公理、平移的性质和平行线的判定与性质,熟练掌握性质与定理是解决此类问题的关键.注意平行公理是:过直线外一点有且只有一条直线与已知直线平行.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:选择题
| x | … | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y | … | -3.5 | -1 | 0.5 | 1 | 0.5 | -1 | -3.5 | … |
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
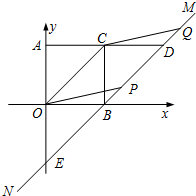 如图,在平面直角坐标系xOy内,?AOBC的顶点A、O、B、C的坐标分别为(0,1)、(0,0)、(1,0)、(1、1),过点B的直线MN与OC平行,AC的延长线交MN于点D,点P是直线MN上的一个动点,CQ∥OP交MN于点Q.
如图,在平面直角坐标系xOy内,?AOBC的顶点A、O、B、C的坐标分别为(0,1)、(0,0)、(1,0)、(1、1),过点B的直线MN与OC平行,AC的延长线交MN于点D,点P是直线MN上的一个动点,CQ∥OP交MN于点Q.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在中超联赛期间,一队员在距离球门12米处挑射,正好射中了2.4米高的横梁,已知球的最高点距球门的水平距离为3米,若足球运行的路线是抛物线,如图,求其函数解析式.
在中超联赛期间,一队员在距离球门12米处挑射,正好射中了2.4米高的横梁,已知球的最高点距球门的水平距离为3米,若足球运行的路线是抛物线,如图,求其函数解析式.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
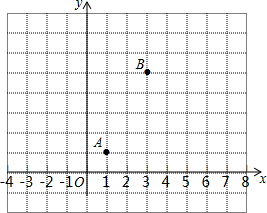 如图,在坐标系中,已知A(1,1)、B(3,5),要在y轴上找一点P,使|PB-PA|最大,则点P的坐标为( )
如图,在坐标系中,已知A(1,1)、B(3,5),要在y轴上找一点P,使|PB-PA|最大,则点P的坐标为( )| A. | (0,1) | B. | (0,2) | C. | $(\frac{4}{3},0)$ | D. | (0,-1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com