
【题目】如图,等边△ABC的边长为5,点D,P,L分别在边AB,BC,CA上,AD=BP=CL=x(x>0).按如图方式作边长均为3的等边△DEF,△PQR,△LMN,点F,R,N分别在射线DA,PB,LC上.
①当边DE,PQ,LM与△ABC的三边围成的图形是正六边形时,x=_____;
②当点D与点B重合时,EF,QR,MN所围成的三角形的周长为_____.

【答案】![]() 3
3
【解析】
(1)利用正六边形的性质,构建方程即可解决问题.
(2)画出图形,可知EF,QR,MN所围成的△OGH是边长为1的等边三角形,由此即可解决问题.
(1)∵等边△ABC中,∠ABC=∠BAC=∠ACB=60°,等边△DEF,△PQR,△LMN中,∠EDF=∠QPR=∠MLN=60°,
∴ADX,BYP,CZL都是等边三角形,
∵AD=BP=CL=x(x>0),
∴AX=DX=BY=PY=CZ=LZ=x,
∴DY=PZ=LX=5﹣2x,
当边DE,PQ,LM与△ABC的三边围成的图形是正六边形时,5﹣2x=x,
∴x=![]() ,
,
故答案为:![]() ;
;
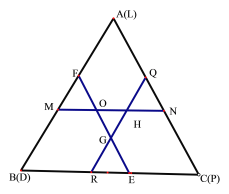
(2)当点D与点B重合时,设EF、QR、MN所围成的三角形为△OGH,由题意可知:△OFM,△EGR,△NHQ都是等边三角形,BE=BF=FE=AM=AN=MN=CQ=CR=QR=3,
∴FM=ER=QN=3+3-5=1,
∴OF=OM=EG=RG=HN=HQ=1,
∴OG=GH=OH=3-1-1=1,
∴OG+GH+OH=3,
即:EF,QR,MN所围成的等边三角形的周长为3.
故答案为3.
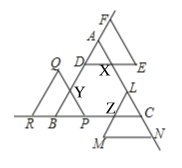


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某景区内有一块矩形油菜花田地(数据如图示,单位:m.)现在其中修建一条观花道(图中阴影部分)供游人赏花.设改造后剩余油菜花地所占面积为ym2.
(1)求y与x的函数表达式;
(2)若改造后观花道的面积为13m2,求x的值;
(3)若要求 0.5≤ x ≤1,求改造后剩余油菜花地所占面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是长为10m,倾斜角为30°的自动扶梯,平台BD与大楼CE垂直,且与扶梯AB的长度相等,在B处测得大楼顶部C的仰角为65°,求大楼CE的高度(结果保留整数).(参考数据:sin65°=0.90,tan65°=2.14)

查看答案和解析>>
科目:初中数学 来源: 题型:
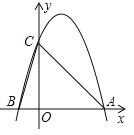
【题目】如图所示,二次函数![]() 的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.
的图象与x轴的一个交点为A(3,0),另一个交点为B,且与y轴交于点C.
(1)求m的值;
(2)求点B的坐标;
(3)该二次函数图像上有一点D(x,y)(其中![]() ,
,![]() ),使
),使![]() ,求点D的坐标.
,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
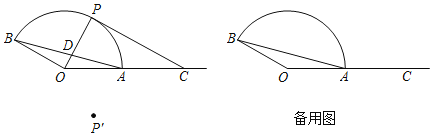
【题目】如图,OA=4,C是射线OA上一点,以O为圆心,OA的长为半径作![]() 使∠AOB=152°,P是
使∠AOB=152°,P是![]() 上一点,OP与AB相交于点D,点P′与P关于直线OA对称,连接CP,
上一点,OP与AB相交于点D,点P′与P关于直线OA对称,连接CP,
尝试:
(1)点P′在![]() 所在的圆 (填“内”“上”或“外”);
所在的圆 (填“内”“上”或“外”);
(2)AB= .
发现:
(1)PD的最大值为 ;
(2)当![]() =2π,∠OCP=28时,判断CP与
=2π,∠OCP=28时,判断CP与![]() 所在圆的位置关系探究当点P′与AB的距离最大时,求AP的长.(注:sin76°=cos14°=
所在圆的位置关系探究当点P′与AB的距离最大时,求AP的长.(注:sin76°=cos14°=![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD中,AB=2,AD=3,O为边AD上一点,以O为圆心,OA为半径r作⊙O,过点B作⊙O的切线BF,F为切点.
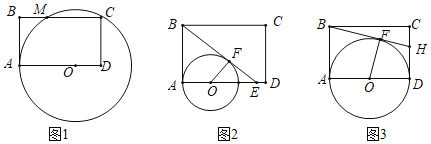
(1)如图1,当⊙O经过点C时,求⊙O截边BC所得弦MC的长度;
(2)如图2,切线BF与边AD相交于点E,当FE=FO时,求r的值;
(3)如图3,当⊙O与边CD相切时,切线BF与边CD相交于点H,设△BCH、四边形HFOD、四边形FOAB的面积分别为S1、S2、S3,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
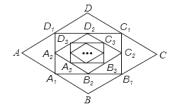
【题目】如图,在菱形![]() 中,边长为10,
中,边长为10,![]() .顺次连结菱形
.顺次连结菱形![]() 各边中点,可得四边形
各边中点,可得四边形![]() ;顺次连结四边形
;顺次连结四边形![]() 各边中点,可得四边形
各边中点,可得四边形![]() ;顺次连结四边形
;顺次连结四边形![]() 各边中点,可得四边形
各边中点,可得四边形![]() ;按此规律继续下去….则四边形
;按此规律继续下去….则四边形![]() 的周长是_________.
的周长是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
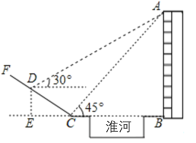
【题目】如图,在淮河的右岸边有一高楼,左岸边有一坡度![]() 的山坡
的山坡![]() ,点
,点![]() 与点
与点![]() 在同一水平面上,
在同一水平面上,![]() 与
与![]() 在同一平面内.某数学兴趣小组为了测量楼
在同一平面内.某数学兴趣小组为了测量楼![]() 的高度,在坡底
的高度,在坡底![]() 处测得楼顶
处测得楼顶![]() 的仰角为
的仰角为![]() ,然后沿坡面
,然后沿坡面![]() 上行了
上行了![]() 米到达点
米到达点![]() 处,此时在
处,此时在![]() 处测得楼顶
处测得楼顶![]() 的仰角为
的仰角为![]() ,求楼
,求楼![]() 的高度.(结果保留整数)(参考数
的高度.(结果保留整数)(参考数![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com