
【题目】如图,在△ABC中,O是AB边上的点,以O为圆心,OB为半径的⊙0与AC相切于点D,BD平分∠ABC,AD=![]() OD,AB=12,求CD的长.
OD,AB=12,求CD的长.
【答案】CD=2![]() .
.
【解析】
由切线的性质得出AC⊥OD,求出∠A=30°,证出∠ODB=∠CBD,得出OD∥BC,得出∠C=∠ADO=90°,由直角三角形的性质得出∠ABC=60°,BC=![]() AB=6,得出∠CBD=30°,再由直角三角形的性质即可得出结果.
AB=6,得出∠CBD=30°,再由直角三角形的性质即可得出结果.
∵⊙O与AC相切于点D,
∴AC⊥OD,
∴∠ADO=90°,
∵AD=![]() OD,
OD,
∴tanA=![]() =
=![]() ,
,
∴∠A=30°,
∵BD平分∠ABC,
∴∠OBD=∠CBD,
∵OB=OD,
∴∠OBD=∠ODB,
∴∠ODB=∠CBD,
∴OD∥BC,
∴∠C=∠ADO=90°,
∴∠ABC=60°,
∴BC=![]() AB=6,
AB=6,
∴∠CBD=![]() ∠ABC=30°,
∠ABC=30°,
∴CD=![]() BC=
BC=![]() ×6=2
×6=2![]() .
.


科目:初中数学 来源: 题型:
【题目】综合与探究
问题情境:
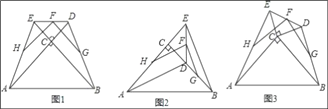
(1)如图1,两块等腰直角三角板△ABC和△ECD如图所示摆放,其中∠ACB=∠DCE=90°,点F,H,G分别是线段DE,AE,BD的中点,A,C,D和B,C,E分别共线,则FH和FG的数量关系是 ,位置关系是 .
合作探究:
(2)如图2,若将图1中的△DEC绕着点C顺时针旋转至A,C,E在一条直线上,其余条件不变,那么(1)中的结论还成立吗?若成立,请证明,若不成立,请说明理由.
(3)如图3,若将图1中的△DEC绕着点C顺时针旋转一个锐角,那么(1)中的结论是否还成立?若成立,请证明,若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题呈现)阿基米德折弦定理:
如图1,AB和BC是⊙O的两条弦(即折线ABC是圆的一条折弦),BC>AB,点M是![]() 的中点,则从M向BC所作垂线的垂足D是折弦ABC的中点,即CD=DB+BA.下面是运用“截长法”证明CD=DB+BA的部分证明过程.
的中点,则从M向BC所作垂线的垂足D是折弦ABC的中点,即CD=DB+BA.下面是运用“截长法”证明CD=DB+BA的部分证明过程.
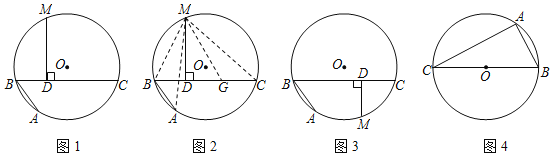
证明:如图2,在CD上截取CG=AB,连接MA、MB、MC和MG.
∵M是![]() 的中点,
的中点,
∴MA=MC①
又∵∠A=∠C②
∴△MAB≌△MCG③
∴MB=MG
又∵MD⊥BC
∴BD=DG
∴AB+BD=CG+DG
即CD=DB+BA
根据证明过程,分别写出下列步骤的理由:
① ,
② ,
③ ;
(理解运用)如图1,AB、BC是⊙O的两条弦,AB=4,BC=6,点M是![]() 的中点,MD⊥BC于点D,则BD= ;
的中点,MD⊥BC于点D,则BD= ;
(变式探究)如图3,若点M是![]() 的中点,(问题呈现)中的其他条件不变,判断CD、DB、BA之间存在怎样的数量关系?并加以证明.
的中点,(问题呈现)中的其他条件不变,判断CD、DB、BA之间存在怎样的数量关系?并加以证明.
(实践应用)根据你对阿基米德折弦定理的理解完成下列问题:
如图4,BC是⊙O的直径,点A圆上一定点,点D圆上一动点,且满足∠DAC=45°,若AB=6,⊙O的半径为5,求AD长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中的两个图形
中的两个图形![]() 与
与![]() ,给出如下定义:
,给出如下定义:![]() 为图形
为图形![]() 上任意一点,
上任意一点,![]() 为图形
为图形![]() 上任意一点,如果
上任意一点,如果![]() 两点间的距离有最小值,那么称这个最小值为图形
两点间的距离有最小值,那么称这个最小值为图形![]() 间的“和睦距离”,记作
间的“和睦距离”,记作![]() ,若图形
,若图形![]() 有公共点,则
有公共点,则![]() .
.
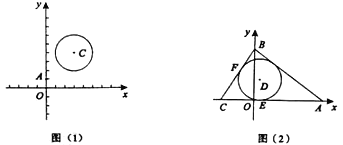
(1)如图(1),![]() ,
,![]() ,⊙
,⊙![]() 的半径为2,则
的半径为2,则![]() ,
,![]() ;
;
(2)如图(2),已知![]() 的一边
的一边![]() 在
在![]() 轴上,
轴上,![]() 在
在![]() 上,且
上,且![]() ,
,![]() ,
,![]() .
.
①![]() 是
是![]() 内一点,若
内一点,若![]() 、
、![]() 分别且⊙
分别且⊙![]() 于E、F,且
于E、F,且![]() ,判断
,判断![]() 与⊙
与⊙![]() 的位置关系,并求出
的位置关系,并求出![]() 点的坐标;
点的坐标;
②若以![]() 为半径,①中的
为半径,①中的![]() 为圆心的⊙
为圆心的⊙![]() ,有
,有![]() ,
,![]() ,直接写出
,直接写出![]() 的取值范围 .
的取值范围 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O是等腰Rt△ABC的外接圆,点D是![]() 上一点,BD交AC于点E,若BC=4,AD=
上一点,BD交AC于点E,若BC=4,AD=![]() ,则AE的长是( )
,则AE的长是( )
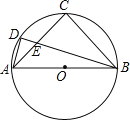
A. 1 B. 1.2 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图以正五边形ABCDE的顶点A为圆心,AE为半径作圆弧交BA的延长线于点A′,再以点B为圆心,BA′为半径作圆弧交CB的延长线于B′,依次进行.得到螺旋线,再顺次连结EA′,AB′,BC′,CD′,DE′,得到5块阴影区域,若记它们的面积分别为S1,S2,S3,S4,S5,且满足S5﹣S2=1,则S4﹣S3的值为( )
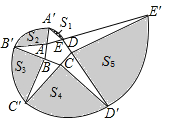
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
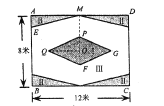
【题目】如图,某校准备给长12米,宽8米的矩形![]() 室内场地进行地面装饰,现将其划分为区域Ⅰ(菱形
室内场地进行地面装饰,现将其划分为区域Ⅰ(菱形![]() ),区域Ⅱ(4个全等的直角三角形),剩余空白部分记为区域Ⅲ;点
),区域Ⅱ(4个全等的直角三角形),剩余空白部分记为区域Ⅲ;点![]() 为矩形和菱形的对称中心,
为矩形和菱形的对称中心,![]() ,
,![]() ,
,![]() ,为了美观,要求区域Ⅱ的面积不超过矩形
,为了美观,要求区域Ⅱ的面积不超过矩形![]() 面积的
面积的![]() ,若设
,若设![]() 米.
米.
甲 | 乙 | 丙 | |
单价(元/米2) |
|
|
|
(1)当![]() 时,求区域Ⅱ的面积.
时,求区域Ⅱ的面积.
(2)计划在区域Ⅰ,Ⅱ分别铺设甲,乙两款不同的深色瓷砖,区域Ⅲ铺设丙款白色瓷砖,
①在相同光照条件下,当场地内白色区域的面积越大,室内光线亮度越好.当![]() 为多少时,室内光线亮度最好,并求此时白色区域的面积.
为多少时,室内光线亮度最好,并求此时白色区域的面积.
②三种瓷砖的单价列表如下,![]() 均为正整数,若当
均为正整数,若当![]() 米时,购买三款瓷砖的总费用最少,且最少费用为7200元,此时
米时,购买三款瓷砖的总费用最少,且最少费用为7200元,此时![]() __________,
__________,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有四张质地完全相同的卡片,正面分别写有四个角度,现将这四张卡片洗匀后,背面朝上.
(1)若从中任意抽取--张,求抽到锐角卡片的概宰;
(2)若从中任意抽取两张,求抽到的两张角度恰好互补的概率.
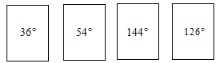
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边△ABC的边长为5,点D,P,L分别在边AB,BC,CA上,AD=BP=CL=x(x>0).按如图方式作边长均为3的等边△DEF,△PQR,△LMN,点F,R,N分别在射线DA,PB,LC上.
①当边DE,PQ,LM与△ABC的三边围成的图形是正六边形时,x=_____;
②当点D与点B重合时,EF,QR,MN所围成的三角形的周长为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com