
ЁОЬтФПЁПШчЭМЃЌвбжЊЫФБпаЮ![]() ЪЧЦНааЫФБпаЮЃЌЕу
ЪЧЦНааЫФБпаЮЃЌЕу![]() КЭ
КЭ![]() дк
дк![]() жсЩЯЃЌЧв
жсЩЯЃЌЧв![]() ЮЊзјБъдЕуЃЌЕу
ЮЊзјБъдЕуЃЌЕу![]() ЃЌКЭЕу
ЃЌКЭЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ВЂбгГЄНЛ
ВЂбгГЄНЛ![]() жсгкЕу
жсгкЕу![]() ЃЎ
ЃЎ
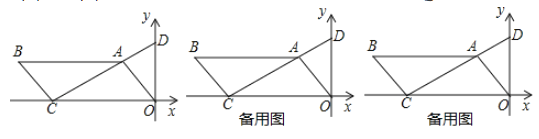
(1)ЧѓжБЯп![]() ЕФНтЮіЪНЃЛ
ЕФНтЮіЪНЃЛ
(2)ШєЕу![]() Дг
Дг![]() ГіЗЂвд2ИіЕЅЮЛ/УыЕФЫйЖШби
ГіЗЂвд2ИіЕЅЮЛ/УыЕФЫйЖШби![]() жсЯђгвдЫЖЏЃЌЭЌЪБЕу
жсЯђгвдЫЖЏЃЌЭЌЪБЕу![]() Дг
Дг![]() ГіЗЂЃЌвд1ИіЕЅЮЛ/УыЕФЫйЖШби
ГіЗЂЃЌвд1ИіЕЅЮЛ/УыЕФЫйЖШби![]() жсЯђзѓдЫЖЏЃЌЙ§Еу
жсЯђзѓдЫЖЏЃЌЙ§Еу![]() ЃЌ
ЃЌ![]() ЗжБ№зї
ЗжБ№зї![]() жсЕФДЙЯпНЛЩфЯп
жсЕФДЙЯпНЛЩфЯп![]() КЭЩфЯп
КЭЩфЯп![]() ЗжБ№гкЕу
ЗжБ№гкЕу![]() ЃЌ
ЃЌ![]() ЃЌЧыВТЯыЫФБпаЮ
ЃЌЧыВТЯыЫФБпаЮ![]() ЕФаЮзДЃЌ(Еу
ЕФаЮзДЃЌ(Еу![]() ЃЌ
ЃЌ![]() жиКЯГ§Эт)ЃЌВЂжЄУїФуЕФНсТлЃЎ
жиКЯГ§Эт)ЃЌВЂжЄУїФуЕФНсТлЃЎ
(3)дк(2)ЕФЬѕМўЯТЃЌЕБЕу![]() дЫЖЏЖрЩйУыЪБЃЌЫФБпаЮ
дЫЖЏЖрЩйУыЪБЃЌЫФБпаЮ![]() ЪЧе§ЗНаЮ?жБНгаДГіНсТлЃЎ
ЪЧе§ЗНаЮ?жБНгаДГіНсТлЃЎ
ЁОД№АИЁПЃЈ1ЃЉжБЯпACЕФНтЮіЪНЮЊ![]() ЃЛЃЈ2ЃЉЫФБпаЮPEFQЪЧОиаЮЃЌжЄУїМћНтЮіЃЛЃЈ3ЃЉЕуPдЫЖЏ
ЃЛЃЈ2ЃЉЫФБпаЮPEFQЪЧОиаЮЃЌжЄУїМћНтЮіЃЛЃЈ3ЃЉЕуPдЫЖЏ![]() УыЛђ
УыЛђ![]() УыЪБЃЌЫФБпаЮEPQFЪЧе§ЗНаЮ
УыЪБЃЌЫФБпаЮEPQFЪЧе§ЗНаЮ
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУД§ЖЈЯЕЪ§ЗЈМДПЩЧѓГіжБЯпACЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЯШРћгУД§ЖЈЯЕЪ§ЗЈЧѓГіжБЯпOAЕФНтЮіЪНЃЌНјЖјЧѓГіЕуEЃЌFзјБъЃЌМДПЩЕУГіPE=FQЃЌМДПЩЕУГіНсТлЃЛ
ЃЈ3ЃЉЯШЗжСНжжЧщПіЃЈЕуQдкЕуPзѓВрЛђгвВрЃЉЧѓГіPQЃЌРћгУPE=PQНЈСЂЗНГЬМДПЩЧѓГіЪБМфЃЎ
НтЃКЃЈ1ЃЉЩшжБЯпACЕФНтЮіЪНЮЊ![]()
ЁпЫФБпаЮABCOЪЧЦНааЫФБпаЮЃЌЧв![]() ЃЌ
ЃЌ![]()
ЁрOC=AB=9
ЁрCЃЈ-9ЃЌ0ЃЉ
Аб![]() ЁЂCЃЈ-9ЃЌ0ЃЉДњШы
ЁЂCЃЈ-9ЃЌ0ЃЉДњШы![]() ЕУЃК
ЕУЃК
Ёр![]()
Ёр![]()
ЁржБЯпACЕФНтЮіЪНЮЊ![]()
ЃЈ2ЃЉЃЉЫФБпаЮPEFQЪЧОиаЮЃЌРэгЩШчЯТЃК
ШчЭМ

ЁпЕуAЕФзјБъЮЊЃЈ-3ЃЌ3ЃЉ
ЁржБЯпOAЕФНтЮіЪНЮЊ![]()
ЁпЕуQДгЕуOГіЗЂвд1ИіЕЅЮЛ/УыбиxжсЯђзѓдЫЖЏ
ЁрOQ=-t
ЁрFЃЈ-tЃЌtЃЉ
ЁрFQ=t
ЁпЕуQДгЕуOГіЗЂвд1ИіЕЅЮЛ/УыбиxжсЯђзѓдЫЖЏЃЌ
ЁрOQ=-tЃЌ
ЁрFЃЈ-tЃЌtЃЉЃЌ
ЁрFQ=tЃЌ
ЁпЕуPДгЕуCГіЗЂвд2ИіЕЅЮЛ/УыбиxжсЯђгвдЫЖЏЃЌ
ЁрCP=2tЃЌ
ЁрOP=-9+2tЃЌ
гЩЃЈ1ЃЉжЊЃЌжБЯпACЕФНтЮіЪНЮЊ![]()
ЁрEЃЈ-9+2tЃЌtЃЉЃЌ
ЁрPE=tЃЌ
ЁрPE=FQЃЌ
ЁпFQЁЭxжсЃЌPEЁЭxжсЃЌ
ЁрЁЯPQF=90ЁуЃЌFQЁЮPEЃЌ
ЁпPE=FQЃЌ
ЁрЫФБпаЮPEFQЪЧЦНааЫФБпаЮЃЌ
ЁпЁЯPQF=90ЁуЃЌ
ЁрЦНааЫФБпаЮPEFQЪЧОиаЮ
ЁрЫФБпаЮPEFQЪЧОиаЮЃЛ
ЃЈ3ЃЉгЩЃЈ2ЃЉжЊЃЌPC=2tЃЌOQ=tЃЌPE=tЃЌ
ЁрPQ=OC-OQ-CP=9-t-2t=9-3tЃЌЛђPQ=OQ+CP-OC=3t-9ЃЌ
ЁпЫФБпаЮPEFQЪЧе§ЗНаЮЃЌ
ЁрPQ=PEЃЌ
Ёр9-3t=tЛђ3t-9=tЃЌ
Ёр![]() Лђ
Лђ![]() ЃЌМДЕуPдЫЖЏ
ЃЌМДЕуPдЫЖЏ![]() УыЛђ
УыЛђ![]() УыЪБЃЌЫФБпаЮEPQFЪЧе§ЗНаЮ
УыЪБЃЌЫФБпаЮEPQFЪЧе§ЗНаЮ


 ФмПМЪдЦкФЉГхДЬОэЯЕСаД№АИ
ФмПМЪдЦкФЉГхДЬОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМABЪЧАыдВЕФжБОЖЃЌЭМ1жаЃЌЕуCдкАыдВЭтЃЛЭМ2жаЃЌЕуCдкАыдВФкЃЌЧыНігУЮоПЬЖШЕФжБГпАДвЊЧѓЛЭМЃЎ
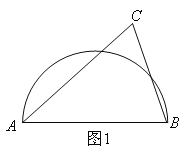
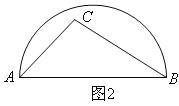
ЃЈ1ЃЉдкЭМ1жаЃЌЛГіЁїABCЕФШ§ЬѕИпЕФНЛЕуЃЛ
ЃЈ2ЃЉдкЭМ2жаЃЌЛГіЁїABCжаABБпЩЯЕФИпЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABCDЕФЖдНЧЯпACЁЂBDНЛгкЕуOЃЌAEЦНЗжЁЯBADНЛBCгкЕуEЃЌЧвЁЯADC=60ЁуЃЌAB=![]() BCЃЌСЌНгOEЃЎЯТСаНсТлЃКЂйЁЯCAD=30ЁуЃЛЂкSABCD=ABACЃЛЂлOB=ABЃЛЂмOE=
BCЃЌСЌНгOEЃЎЯТСаНсТлЃКЂйЁЯCAD=30ЁуЃЛЂкSABCD=ABACЃЛЂлOB=ABЃЛЂмOE=![]() BCЃЌГЩСЂЕФИіЪ§гаЃЈЁЁЁЁЃЉ
BCЃЌГЩСЂЕФИіЪ§гаЃЈЁЁЁЁЃЉ

A. 1Иі B. 2Иі C. 3Иі D. 4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЮЊСЫСЫНтОХФъМЖбЇЩњЬхг§ВтЪдГЩМЈЧщПіЃЌвдОХФъМЖЃЈ1ЃЉАрбЇЩњЕФЬхг§ВтЪдГЩМЈЮЊбљБОЃЌАДBЁЂCЁЂDЫФИіЕШМЖНјааЭГМЦЃЌВЂНЋЭГМЦНсЙћЛцжЦШчЯТСНЗљЭГМЦЭМЃЌЧыФуНсКЯЭМжаЫљИјаХЯЂНтД№ЯТСаЮЪЬтЃКЃЈЫЕУїЃКAМЖЃК90ЗжЉ100ЗжЃЛBМЖЃК75ЗжЉ89ЗжЃЛCМЖЃК60ЗжЁЋ74ЗжЃЛDМЖЃК60ЗжвдЯТЃЉ
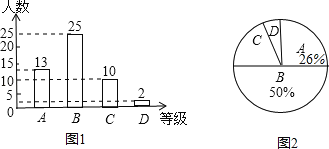
ЃЈ1ЃЉЧѓГіDМЖбЇЩњЕФШЫЪ§еМШЋАрзмШЫЪ§ЕФАйЗжБШЃЛ
ЃЈ2ЃЉЧѓГіЩШаЮЭГМЦЭМЃЈЭМ2ЃЉжаCМЖЫљдкЕФЩШаЮдВаФНЧЕФЖШЪ§ЃЛ
ЃЈ3ЃЉШєИУаЃОХФъМЖбЇЩњЙВга500ШЫЃЌЧыФуЙРМЦетДЮПМЪджаAМЖКЭBМЖЕФбЇЩњЙВгаЖрЩйШЫЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПе§ЗНаЮ![]() ЁЂе§ЗНаЮ
ЁЂе§ЗНаЮ![]() ШчЭМЗХжУЃЌЕу
ШчЭМЗХжУЃЌЕу![]() дкЭЌвЛЬѕжБЯпЩЯЃЌЕу
дкЭЌвЛЬѕжБЯпЩЯЃЌЕу![]() дк
дк![]() БпЩЯЃЌ
БпЩЯЃЌ![]() ЃЌЧв
ЃЌЧв![]() ЃЌСЌНс
ЃЌСЌНс![]() НЛ
НЛ![]() гк
гк![]() ЃЌгаЯТСаНсТлЃКЂй
ЃЌгаЯТСаНсТлЃКЂй![]() ЃЛЂк
ЃЛЂк![]() ЃЛЂл
ЃЛЂл![]() ЃЛЂм
ЃЛЂм![]() ЃЛЂн
ЃЛЂн![]() ЃЎвдЩЯНсТле§ШЗЕФИіЪ§га( )
ЃЎвдЩЯНсТле§ШЗЕФИіЪ§га( )
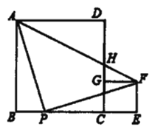
A.5ИіB.4ИіC.3ИіD.2Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПАЫФъМЖЃЈ1ЃЉАрбаОПадбЇЯАаЁзщЮЊбаОПШЋаЃЭЌбЇПЮЭтдФЖСЧщПіЃЌдкШЋаЃЫцЛњбћЧыСЫВПЗжЭЌбЇВЮгыЮЪОэЕїВщЃЌЭГМЦЭЌбЇУЧвЛИідТдФЖСПЮЭтЪщЕФЪ§СПЃЌВЂЛцжЦСЫШчЯТЕФЭГМЦЭМ1КЭЭМ2ЃЌЧыИљОнЭМжаЯрЙиаХЯЂЃЌНтОіЯТСаЮЪЬтЃК

ЃЈЂёЃЉЭМ1жа![]() ЕФжЕЮЊ____________ЃЌЙВга____________УћЭЌбЇВЮгыЮЪОэЕїВщЃЛ
ЕФжЕЮЊ____________ЃЌЙВга____________УћЭЌбЇВЮгыЮЪОэЕїВщЃЛ
ЃЈЂђЃЉЧѓЭГМЦЕФетзщЪ§ОнЕФЦНОљЪ§ЁЂжкЪ§КЭжаЮЛЪ§ЃЛ
ЃЈЂѓЃЉШЋаЃЙВгабЇЩњ1500ШЫЃЌИљОнбљБОЪ§ОнЃЌЙРМЦИУаЃбЇЩњвЛИідТдФЖС2БОПЮЭтЪщЕФШЫЪ§дМЮЊЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
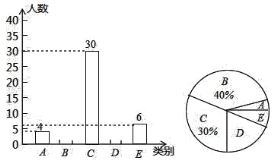
ЁОЬтФПЁПЮЊЙцЗЖбЇЩњЕФдкаЃБэЯжЃЌЮваЃФГАрЪЕааСЫВйааЦРЗжжЦЃЌИљОнбЇЩњЕФВйааЗжИпЕЭЗжЮЊ![]() ЮхИіЕШМЖЃЌЯжЖдИУАрБОбЇЦкЕФВйааЕШМЖНјааСЫЭГМЦЃЌВЂЛцжЦСЫВЛЭъећЕФСНжжЭГМЦЭМЃЌЧыИљОнЭМЯѓЛиД№ЮЪЬтЃК
ЮхИіЕШМЖЃЌЯжЖдИУАрБОбЇЦкЕФВйааЕШМЖНјааСЫЭГМЦЃЌВЂЛцжЦСЫВЛЭъећЕФСНжжЭГМЦЭМЃЌЧыИљОнЭМЯѓЛиД№ЮЪЬтЃК
ЃЈ1ЃЉ![]() РрЫљЖдгІЕФдВаФНЧЪЧ_________ЖШЃЌбљБОжаГЩМЈЕФжаЮЛЪ§Тфдк_________РржаЃЌВЂВЙШЋЬѕаЮЭГМЦЭМЃЛ
РрЫљЖдгІЕФдВаФНЧЪЧ_________ЖШЃЌбљБОжаГЩМЈЕФжаЮЛЪ§Тфдк_________РржаЃЌВЂВЙШЋЬѕаЮЭГМЦЭМЃЛ
ЃЈ2ЃЉШє![]() РрКЌга2УћФаЩњКЭ2УћХЎЩњЃЌЫцЛњбЁдё2УћбЇЩњВЮМгЯТбЇЦкПЊбЇЕФЁАЙњЦьЯТЕФНВЛАЁБбнНВЛюЖЏЃЌЧыгУСаБэЗЈЛђЛЪїзДЭМЗЈЧѓЧЁКУГщЕН1УћФаЩњКЭ1УћХЎЩњЕФИХТЪЃЎ
РрКЌга2УћФаЩњКЭ2УћХЎЩњЃЌЫцЛњбЁдё2УћбЇЩњВЮМгЯТбЇЦкПЊбЇЕФЁАЙњЦьЯТЕФНВЛАЁБбнНВЛюЖЏЃЌЧыгУСаБэЗЈЛђЛЪїзДЭМЗЈЧѓЧЁКУГщЕН1УћФаЩњКЭ1УћХЎЩњЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§![]() ЕФЭМЯѓШчЭМЫљЪОЃЌИјГівдЯТНсТлЃК Ђй
ЕФЭМЯѓШчЭМЫљЪОЃЌИјГівдЯТНсТлЃК Ђй![]() ЃЛЂк
ЃЛЂк![]() ЃЛЂл
ЃЛЂл ![]() ЃЛЂм
ЃЛЂм![]() ЃЎЦфжае§ШЗНсТлЕФађКХЪЧЃЈ ЃЉ
ЃЎЦфжае§ШЗНсТлЕФађКХЪЧЃЈ ЃЉ
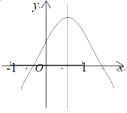
A.ЂлЂмB.ЂкЂмC.ЂкЂлD.ЂйЂкЂл
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвЛДЮКЏЪ§![]() ЕФЭМЯѓгыЗДБШР§КЏЪ§
ЕФЭМЯѓгыЗДБШР§КЏЪ§![]() ЕФЭМЯѓЯрНЛгк
ЕФЭМЯѓЯрНЛгк![]() ЁЂ
ЁЂ![]() СНЕуЃЌЦфжаЕу
СНЕуЃЌЦфжаЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() ЃЌЕу
ЃЌЕу![]() ЕФзјБъЮЊ
ЕФзјБъЮЊ![]() .
.
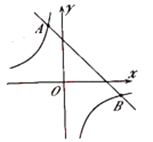
ЃЈ1ЃЉИљОнЭМЯѓЃЌжБНгаДГіТњзу![]() ЕФ
ЕФ![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉЧѓетСНИіКЏЪ§ЕФБэДяЪНЃЛ
ЃЈ3ЃЉЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯЃЌЧв
ЩЯЃЌЧв![]() ЃЌЧѓЕу
ЃЌЧѓЕу![]() ЕФзјБъ.
ЕФзјБъ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com