【题目】已知二次函数y＝
x2﹣3x+4．
（1）配方成y＝a（x﹣h）2+k的形式；
（2）求出它的图象的开口方向对称轴顶点坐标；
（3）求当y＜0时x的取值范围．
【答案】（1）y＝
（x﹣3）2﹣；（2）函数的开口向上，对称轴是直线x＝3，顶点坐标为（3，﹣）；（3）2＜x＜4．
【解析】
(1)根据题目中的函数解析式，利用配方法可以将题目中的函数解析式化为y＝a（x﹣k）2+h的形式，
(2)根据顶点式写出它的开口方向、对称轴及顶点坐标；
(3)求得抛物线与x的交点坐标，根据二次函数的性质写出当y＜0时，x的取值范围．
解：(1)二次函数y＝x2﹣3x+4＝（x﹣3）2﹣，；
(2)∵y＝（x﹣3）2﹣中a＝＞0，
故该函数的开口向上，对称轴是直线x＝3，顶点坐标为（3，﹣）；
(3)当y＝0时，0＝x2﹣3x+4，得x＝2或x＝4，
故y＜0时，x的取值范围是2＜x＜4．
快乐小博士巩固与提高系列答案科目：初中数学 来源： 题型：
【题目】已知二次函数y=ax2+bx+c的图象如图所示，它与x轴的两个交点分别为（﹣1，0），（3，0）．对于下列命题：①b﹣2a=0；②abc＜0；③a﹣2b+4c＜0；④8a+c＞0．其中正确的有（ ）
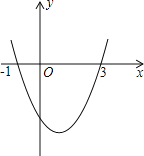
A.3个B.2个C.1个D.0个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知，如图，有一块含有30°的直角三角形
的直角边
的长恰与另一块等腰直角三角形
的斜边
的长相等．把该套三角板放置在平面直角坐标系中，且
（1）若某开口向下的抛物线的顶点恰好为点
，请写出一个满足条件的抛物线的解析式．
（2）若把含30°的直角三角形绕点
按顺时针方向旋转后，斜边
恰好与轴重叠，点落在点
，试求图中阴影部分的面积（结果保留
）
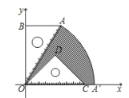
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】为推进扬州市“五个一百工程”活动，小明、小亮、小丽3人分别从A、B两种不同的名著中任意选择一种阅读
（1）小明选择A种名著阅读的概率是 ；
（2）求小明、小亮、小丽3人选择同一种名著阅读的概率（请用画树状图的方法给出分析过程，并求出结果）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】飞机着陆后滑行的距离y（单位：m）关于滑行时间以（单位：）的函数解析式是y＝6t﹣
t2．在飞机着陆滑行中，滑行最后的150m所用的时间是（ ）s．
A.10B.20C.30D.10或30
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，抛物线y＝ax2+bx+c的对称轴为x＝﹣1，且过点（
，0），有下列结论：①abc＞0； ②a﹣2b+4c＞0；③25a﹣10b+4c＝0；④3b+2c＞0；其中所有正确的结论是（ ）
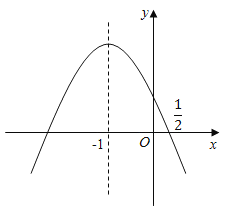
A.①③B.①③④C.①②③D.①②③④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在正方形ABCD中，AB＝4，E是AB上一点，连接DE，过点A作AF⊥DE，垂足为F．⊙O经过点C、D、F，与AD相交于点G，且AB与⊙O相切，则AE的长为_____．
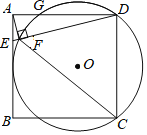
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在“学本课堂”的实践中，王老师经常让学生以“问题”为中心进行自主、合作、探究学习.
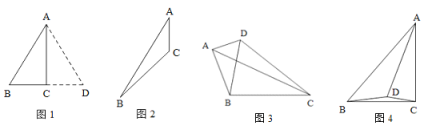
（课堂提问）王老师在课堂中提出这样的问题：如图1，在Rt△ABC中，∠ACB=90°，∠BAC=30°，那么BC和AB有怎样的数量关系？
（互动生成）经小组合作交流后，各小组派代表发言.
（1）小华代表第3小组发言：AB=2BC. 请你补全小华的证明过程.
证明：把△ABC沿着AC翻折，得到△ADC.
∴∠ACD=∠ACB=90°，
∴∠BCD=∠ACD+∠ACB=90°+90°=180°，
即：点B、C、D共线.（请在下面补全小华的证明过程）
（2）受到第3小组“翻折”的启发，小明代表第2小组发言：如图2，在△ABC中，如果把条件“∠ACB=90°”改为“∠ACB=135°”，保持“∠BAC=30°”不变，若BC=1，求AB的长.
（思维拓展）如图3，在四边形ABCD中，∠BCD=45°，∠BAD=90°，∠ADB=∠CDB=60°，且AC=3，则△ABD的周长为 .
（能力提升）如图4，点D是△ABC内一点，AD=AC，∠BAD=∠CAD=20°，∠ADB+∠ACB=210°，则AD、DB、BC三者之间的相等关系是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
