
【题目】如图,在正方形ABCD中,AB=4,E是AB上一点,连接DE,过点A作AF⊥DE,垂足为F.⊙O经过点C、D、F,与AD相交于点G,且AB与⊙O相切,则AE的长为_____.
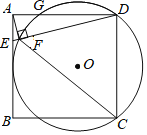
【答案】1
【解析】
设AB与⊙O相切于M,连接OM并反向延长交CD于N,则MN⊥AB,连接GF,根据垂径定理得到CN=DN,根据相似三角形的性质得到![]() =
=![]() ,如图,连接CG,根据相似三角形的性质得到
,如图,连接CG,根据相似三角形的性质得到![]() =
=![]() ,推出AG=EA,根据勾股定理列方程即可得到结论.
,推出AG=EA,根据勾股定理列方程即可得到结论.
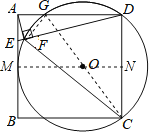
解:设AB与⊙O相切于M,连接OM并反向延长交CD于N,
则MN⊥AB,连接GF,
在正方形ABCD中,∵AB∥CD,
∴MN⊥CD,
∴CN=DN,
∵∠ADC=90°,
∴∠CDF+∠ADF=90°,
∵AF⊥DE,
∴∠AFD=90°,
∴∠DAF+∠ADF=90°,
∴∠DAF=∠CDF,
∵四边形GFCD是⊙O的内接四边形,
∴∠FCD+∠DGF=180°,
∵∠FGA+∠DGF=180°,
∴∠FGA=∠FCD,
∴△AFG∽△DFC,
∴![]() =
=![]() ,
,
如图,连接CG.
∵∠EAD=∠AFD=90°,∠EDA=∠ADF,
∴△EDA∽△ADF,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
在正方形ABCD中,DA=DC,
∴AG=EA,
∴DG=4﹣AE,
∵ON=![]() DG=2﹣
DG=2﹣![]() AE,
AE,
∴CG=2OM=2(4﹣ON)=4+AE,
∵DG2+CD2=CG2,
∴(4﹣AE)2+42=(4+AE)2,
∴AE=1.
故答案为:1.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD中,点P是CD的中点,∠BCD=60°,射线AP交BC的延长线于点E,射线BP交DE于点K,点O是线段BK的中点.
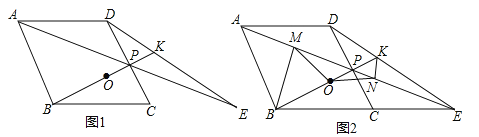
(1)求证:△ADP≌△ECP;
(2)若BP=nPK,试求出n的值;
(3)作BM丄AE于点M,作KN丄AE于点N,连结MO、NO,如图2所示,请证明△MON是等腰三角形,并直接写出∠MON的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
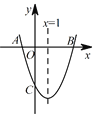
【题目】如图,已知抛物线y=ax2+bx-3的对称轴为直线x=1,交x轴于A,B两点,交y轴于C点,其中B点的坐标为(3,0).
(1)直接写出A点的坐标;
(2)求二次函数y=ax2+bx-3的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=![]() x2﹣3x+4.
x2﹣3x+4.
(1)配方成y=a(x﹣h)2+k的形式;
(2)求出它的图象的开口方向对称轴顶点坐标;
(3)求当y<0时x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
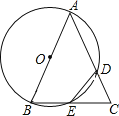
【题目】已知△ABC,以AB为直径的⊙O分别交AC于D,BC于E,连接ED,若ED=EC.
(1)求证:AB=AC;
(2)若AB=4,BC=![]() ,求CD的长.
,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+1与双曲线相交于点A(m,![]() )与x轴交于点 B.
)与x轴交于点 B.
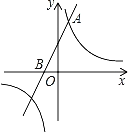
(1)求双曲线的函数表达式:
(2)点P在x轴上,如果△ABP的面积为6,求点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年九龙口诗词大会在九龙口镇召开,我校九年级选拔了3名男生和2名女生参加某分会场的志愿者工作.本次学生志愿者工作一共设置了三个岗位,分别是引导员、联络员和咨询员.
(1)若要从这5名志愿者中随机选取一位作为引导员,求选到女生的概率;
(2)若甲、乙两位志愿者都从三个岗位中随机选择一个,请你用画树状图或列表法求出他们恰好选择同一个岗位的概率.(画树状图和列表时可用字母代替岗位名称)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店准备销售一种多功能旅行背包,计划从厂家以每个30元的价格进货,经过市场发现当每个背包的售价为40元时,月均销量为280个,售价每增长2元,月均销量就相应减少20个.
(1)若使这种背包的月均销量不低于130个,每个背包售价应不高于多少元?
(2)在(1)的条件下,当该这种书包销售单价为多少元时,销售利润是3120元?
(3)这种书包的销售利润有可能达到3700元吗?若能,请求出此时的销售单价;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
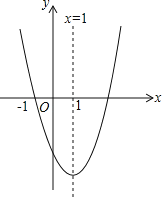
【题目】如图抛物线y=ax2+bx+c的图象经过(﹣1,0),对称轴x=1,则下列三个结论:①abc<0;②10a+3b+c>0;③am2+bm+a≥0.正确的结论为_____(填序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com